Sidereal Time
While solar time is determined from the Earth's rotation relative to the Sun, sidereal time is determined from the Earth's rotation relative to distant stars. Because the Earth does orbit around the Sun in addition to rotation, and thus the position of the Sun between the stars changes for the observer on Earth during the year, solar time and sidereal time differ from each other. In astronomy, it is precisely defined as the hour angle of a spring point, i. e. a point with zero right ascension. If the spring point passes through the local meridian, it is exactly 0 hours local sedireal time. Sidereal time runs a bit faster than solar time. Therefore, one sidereal day is a little shorter than one solar day; it equals 23 h 56 min and 4.09 s of the mean solar time. Sidereal time can be tracked by the position of the constellations in the sky, as shown in the following figure.

(Source: https://commons.wikimedia.org/wiki/File:Grosserwagenmitzeigerz.jpg)
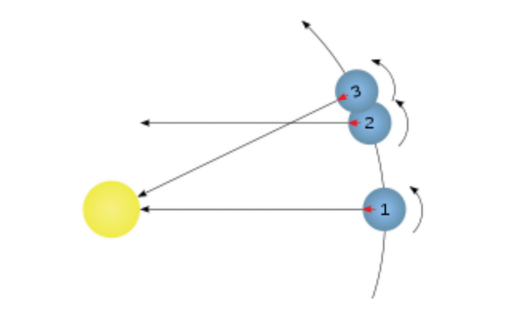
The difference between the length of sidereal and solar time can be approximated by means of the attached schematic picture (in the diagram, the mutual sizes of bodies, their distance and the angle between positions 1 and 3 do not correspond). We start from the position of the Earth marked with the number 1. The Earth moves around the Sun approximately in a circle (it is exactly an ellipse, but only slightly different from a circle) and at the same time rotates around its own axis. The direction of orbit and the Earth's rotation are the same (the moments of momentum of both movements have the same orientation). After the Earth rotates 360 degrees around its axis, it reaches position 2. Between 1 and 2, one sidereal day passed. However, the observer on the Earth's surface does not yet have the Sun in the same position as it was in position 1. Only after further movement around the Sun and simultaneous rotation around its axis will the Earth reach position 3, when the observer has the Sun on the surface of the Earth in the same position as in position 1. One solar day passed between positions 1 and 3. It is therefore clear that a solar day is longer than a sidereal day.
The figure shows the angle between the guides in positions 1 and 3, which corresponds to one solar day. Because the year is about 365 days and the circle corresponds to an angle of 360 degrees, the Earth around the Sun passes an angle of approximately 1 degree each day (more precisely, a slightly smaller angle, equal to 360/365 degrees). The Earth rotates the same angle around its axis, so that one solar day occurs. Therefore, a solar day is longer by the time required to rotate the Earth by one degree, i. e. by 4 minutes (1/360 of a day equals 24 60/360 minutes, which is 4 minutes). Because the angle is slightly less than 1 degree (as mentioned above, it equals 360/365 degrees), the difference between a sidereal and a solar day is slightly less than the calculated 4 minutes (3 min 55.91 s of the mean solar time, or 3 min 56.555 s of the sidereal time).
(Source: https://commons.wikimedia.org/wiki/File:Sidereal_day_(prograde).svg)
It has been agreed that solar and sidereal times have the same value at the time of the autumn equinox.
Note: In addition to the mentioned times, astronomers use other times that are more accurate and free from various influences that disrupt their stable continuous flow.