INTRODUCTION
The units of length that we use in most physical measurements are suitable for measuring objects we encounter in everyday life - maximum dimensions of package that the post office still sends are measured in centimetres, distance to school and to work in kilometres, and so on. For measuring in space we need corresponding units. The distance of the Moon from the Earth can be expressed in kilometres - this distance is approximately 363,300 to 405,500 km. However, the distance of the Sun is hundreds of millions of kilometres, and the distance of the nearest stars would be trillions of kilometres! Therefore, in astronomy we use such units of length that are suitable for measuring cosmic distances.
Measurement of distances in Universe (light year, parsec, parallax)
Astronomical unit
The astronomical unit (1 au) is defined as the mean distance between the centres of the Earth and the Sun. One astronomical unit is approximately 150 million kilometres. According to the definition of the International Astronomical Union, an astronomical unit is understood as he radius of a circular orbit, in which a body of negligible mass, and free of perturbations, would revolve around the Sun at an angular velocity of 0.017 202 098 95 radians per day. Its currently most accurate value is determined by a resolution of the International Astronomical Union of 2009 as 1 au = (149 597 870,700 ± 0,003) km.
Light year
A light year is the distance that light travels in one Julian year in a vacuum: 1 ly = 299 792 456 m·s–1 · 365,25 days · 24 hours · 60 minutes · 60 seconds = 9,461 · 1012 km.
Parallax
Parallax is an angle at which we see a defined length from a star, e.g. an equatorial parallax is the angle at which we would see the diameter of the Earth. Annual parallax p is the angle at which we would see the length 1 au from a given distance (see Fig. 1)
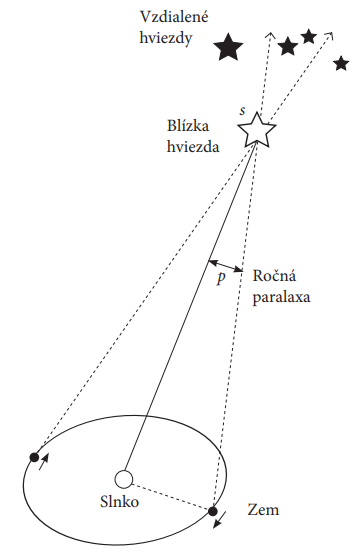
Figure 1 Annual parallax
Parsec
From the astronomical unit is derived the unit of parsec(1 pc, from paralactic second. It is the distance at which one astronomical unit subtends an angle of one arcsecond.
To derive the length of parsec:
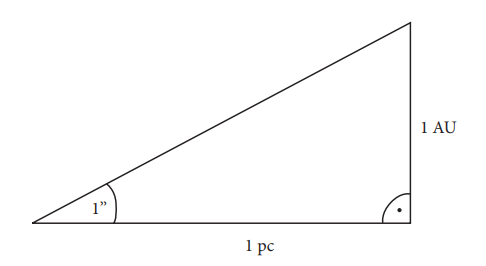
Figure 2 Derivation of parsec length
We can write:
One parsec is approximately 3.2 ly.
If we know the annual parallax pmax of the star (measured according to Fig. 1), its distance r is determined as
where both r and pmax are in curly braces, because such an equation does not fit dimensionally; there is no tangent function in the denominator, because if we substitute pmax in radians, then for such small angles the value of the tangent is directly equal to the angle in radians, and it is not necessary to use trigonometric functions.