Practical Exercise 2: MEASUREMENT OF DISTANCE
In this exercise you will try to measure the distance of an object similar to how distances are measured in astronomy. Choose a clearly visible object, such as a town hall tower, a tall chimney, etc. You will need a tape measure and a compass for measuring (in the worst case, a compass in a mobile phone will be sufficient).
1. Define the measurement base (points A and B in Figure 3). It should not be too small - if you estimate that the object is in the order of kilometres, the base should be in hundreds of meters. The smaller the base, the worse the measurement accuracy. It is good to choose e.g. a turn or a crossing of streets as one of the points, so that the measurement can be verified by means of a satellite map.
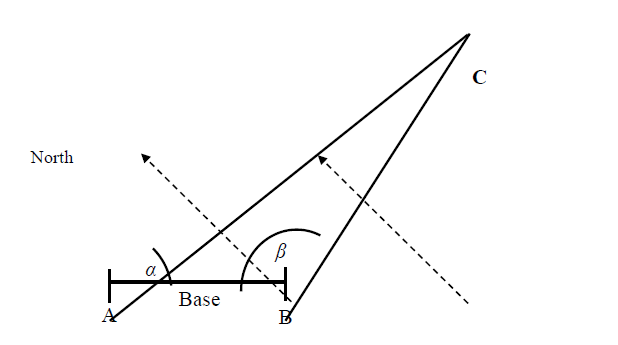
Figure 5 The calculation
2. Use the compass at point A to determine where the north is. Then measure at what angle α you can see the object whose distance you want to measure (see Fig. 3).
3. In the same way determine the north and the angle β at point B.
4. With the known base length |AB| and with the angles α and β according to the asa theorem, construct a triangle ABC, where the point C corresponds to the object whose distance you want to determine. The image should be drawn e.g. at a scale of 1:500 and the distance of the object can be measured in the ABC triangle.
5. Open a suitable online map (example is given in Fig. 6) and verify
a. the length of the base,
b. the distance of the object.
6. Calculate the measurement error according to the formula
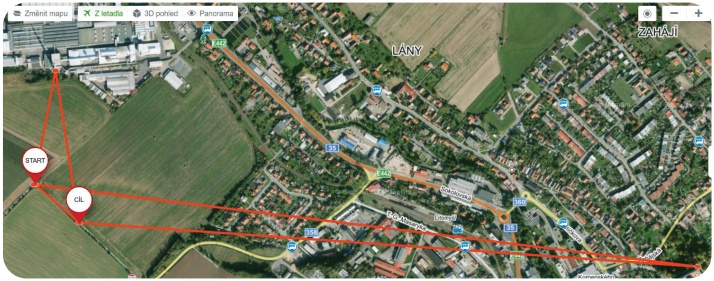
Figure 6 Online map (example)