Practical Exercise 4: SEGMENTED MIRROR
In the described activity, pupils should come to this conclusion themselves while considering the construction of a mirror with a diameter of ten metres. The activity should start with the words: “Your job is to design a ten-metre mirror for a new telescope for less than 7 million dollars.”
Pupils have a graph showing the dependency of the price of the mirror on its diameter:
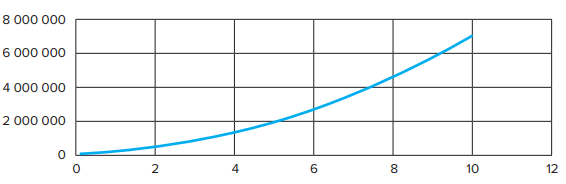
Figure 8: Dependency of the price of a primary mirror on its diameter
Dependency of the price of a primary mirror on its diameter
There is also a worksheet available with circles with diameters of 1, 2.5, 5 and 10 cm, while the 10 cm circle represents a ten-metre mirror. Pupils can cut out these circles and try different mirror configurations. During their experiments, they should find out that it is cheaper to replace one large mirror with a set of smaller mirrors, the total area of which gives the required area of a mirror with a diameter of 10 metres. The total price can be expressed as
where D = 10 m is the diameter of the required mirror, d the diameter of a segment and c the price of one segment according to the graph. Pupils should find out that a large number of smaller mirrors reduces the price. Finally, groups can present their solutions to the class. If at this point one of the pupils thinks that a hexagonal shape of segments is even better, praise the pupil significantly. Otherwise, you can ask why we find hexagonal segments in professional telescopes. It is advisable to use the following figure (which, however, should not be a part of the worksheet):
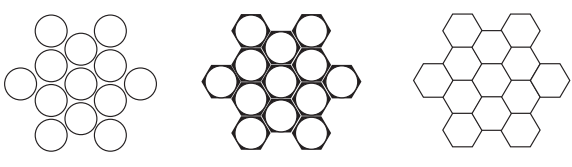
Figure 9