Použití kuželoseček v astronomii. Oběžné dráhy. Dráhové elementy
V astronomii se kuželosečky používají k popisu oběžných drah nebeských těles. Oběžná dráha nebeského tělesa je trajektorie, kterou těleso opisuje v gravitačním poli při pohybu kolem jiného nebeského tělesa (Obr. 4).
V planetárním systému mají všechna tělesa (planety, trpasličí planety, komety, planetky atd.), která jsou gravitačně vázána, eliptické oběžné dráhy, přičemž se v jednom ohnisku (stejném pro všechna tělesa) nachází centrální hvězda. Podobně satelity (přírodní a umělé) mají eliptické oběžné dráhy kolem své mateřské planety (nebo trpasličí planety či planetky), viz obr. 4.
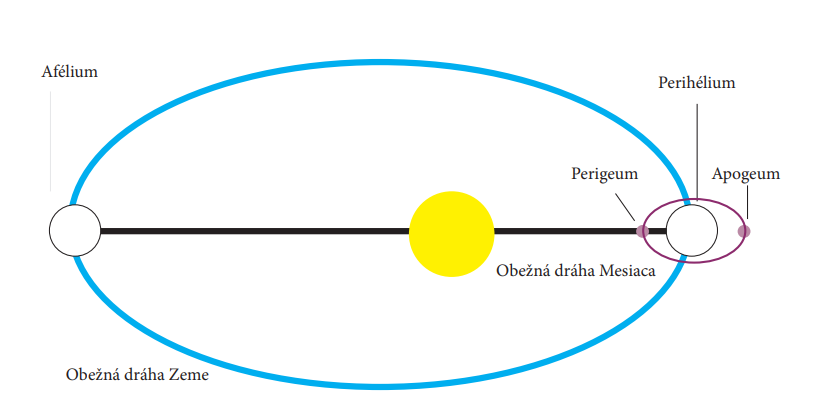
Obr. 4: Oběžná dráha Země kolem Slunce a oběžná dráha Měsíce kolem Země, není v měřítku
(zdroj: NOAA (https://www.nasa.gov/audience/forstudents/5-8/features/nasa-knows/what-is-orbit-58.html)
Bod z oběžné dráhy, ve kterém je těleso nejblíže k Zemi, se nazývá perigeum (přízemí) a bod, ve kterém je těleso od Země nejvíce vzdálené, se nazývá apogeum (odzemí). Pokud jde o pohyb tělesa kolem Slunce, jde o body, které se nazývají perihelium (přísluní) a afélium (odsluní), viz obr. 4; v případě systému dvou hvězd se nazývají periastron a apoastron, a obecně se nazývají periapsida (perifokus) a apoapsida (apofokus). Podobný význam mají pojmy peri-centrum a apocentrum, většinou se zaměňují s apsidami, nicméně vztahují se k nejbližšímu a nejvzdálenějšímu bodu od těžiště soustavy.
Oběžné dráhy planet ve Sluneční soustavě jsou elipsy s malou výstředností (tj. jsou blízko ke kruhovým drahám), přičemž největší je výstřednost oběžné dráhy planety Merkur (e = 0,206) a nejmenší je výstřednost oběžné dráhy planety Venuše (e = 0,007). Naopak, komety mají vysoce výstředné oběžné dráhy. (Obr. 5)
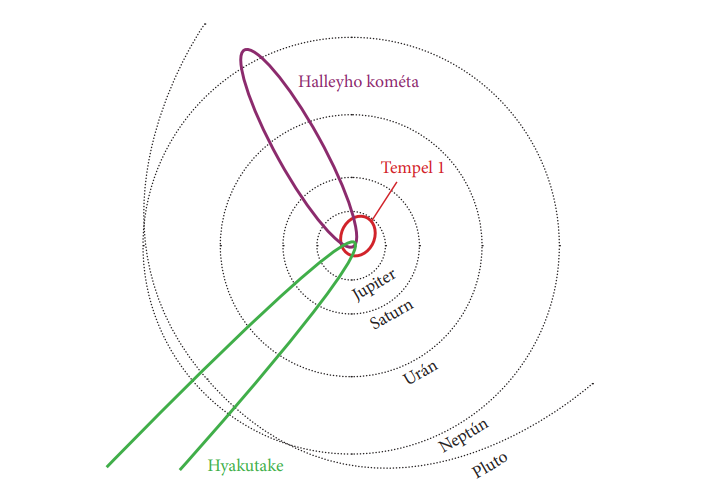
Obr. 5: Porovnání oběžných drah planet Jupiter, Saturn, Uran a Neptun s oběžnou dráhou Hall-eyovy komety, komety Tempel 1 a komety Hyakutake. Je vidět, že oběžné dráhy těchto komet mají mnohem protáhlejší elipsy, tj. mají mnohem větší výstřednost. Zdroj: http://deepimpact.umd.edu/gallery/orbits3.html CREDIT: Tony Farnham
Pro každou oběžnou dráhu existuje soubor para-metrů, které definují její typ, rozměry, orientaci ve vztahu k referenční rovině atd. Nazýváme je dráhové elementy. Při studiu pohybů těles ve Slu-neční soustavě se za referenční rovinu považuje rovina zemské oběžné dráhy nazývaná ekliptika (znázorněna namodralou barvou). (Obr. 6).
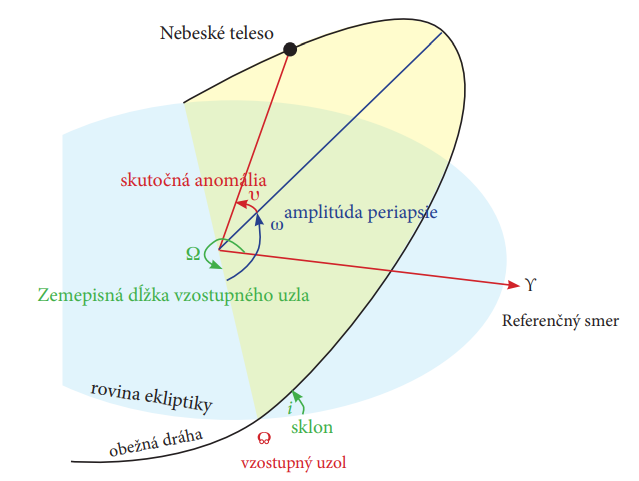
Obr. 6: Dráhové elementy. Rovina oběžné dráhy tělesa je označena žlutou barvou a rovina ekliptiky modrou barvou. Zdroj: Lasunncty at the English Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=8971052
Dráhové elementy eliptické oběžné dráhy
V případě eliptické oběžné dráhy jsou jejími hlavními elementy:
• hlavní poloosa (a) – polovina hlavní osy, která prochází středem a dvěma ohnisky elipsy (Obr. 2); podle třetího Keplerova zákona velikost hlavní poloosy jednoznačně určuje oběžnou dobu (čas potřebný k tomu, aby nebeský objekt vykonal jeden oběh kolem mateřského tělesa). Velikost hlavní poloosy charakterizuje, jak daleko se nachází těleso od centrálního tělesa. Schematické uspořádání těles Sluneční soustavy je znázorněno na obr. 7.
• výstřednost oběžné dráhy (e), která spolu s hlavní poloosou určuje základní rozměry a tvar oběžné dráhy.
• sklon oběžné dráhy (i) je úhel mezi rovinou oběžné dráhy a rovinou ekliptiky (obr. 6). Většina planet Sluneční soustavy má velmi malý sklon (pro Zemi je to samozřejmě nula), mezi 0,8° (pro Uran) a 7° (pro Merkur). Ilustrace je znázorněna na Obr. 8. Mnohem větší sklony oběžných drah jsou u většiny trpasličích planet a komet (například oběžná dráha Pluta má sklon 17° a sklon Eris je dokonce 43°).
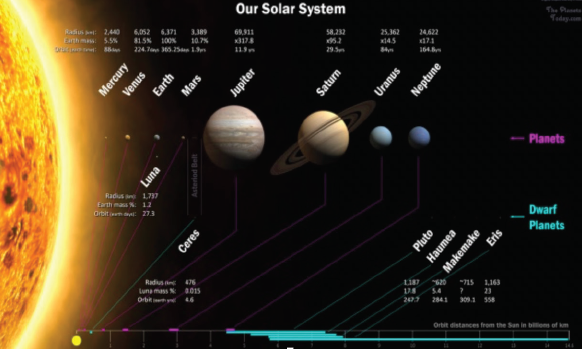
Obr. 7: Schéma Sluneční soustavy. Vzdálenost dané planety nebo obecně tělesa od Slunce závisí na velikosti hlavní poloosy (a výstřednosti) oběžné dráhy planety nebo tělesa.
Kromě hlavní poloosy, výstřednosti a sklonu oběžné dráhy definujeme ještě další tři dráhové elementy, které pomáhají určit prostorovou polohu oběžné dráhy ve vztahu k ekliptice, orientaci oběžné dráhy v její vlastní rovině a průchod tělesa perihéliem. Pokud tedy známe všechny dráhové elementy, můžeme kdykoliv zjistit polohu daného tělesa na oběžné dráze. Nebo naopak, dostatečně dlouhými a přesnými pozorováními nebeského objektu můžeme získat dráhy
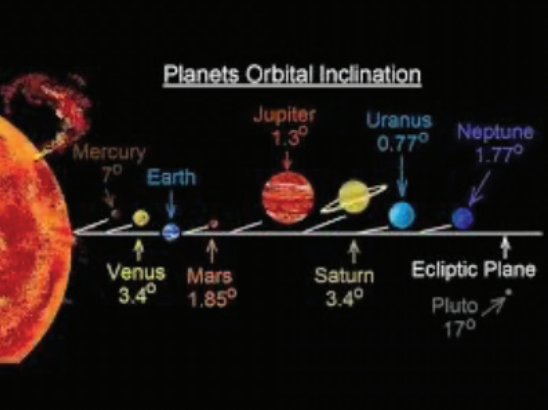
Obr. 8: Sklon oběžných drah planet Sluneční soustavy. Pro srovnání je také uvedena trpasličí planeta Pluto.