Úvod
Kuželosečky jsou jednou z nejstarších a nejdéle studovaných geometrických křivek. Věří se, že je původně objevil Menehm (jeden z učitelů Alexandra Velikého) ve 4. st. př. n. l. Později je studoval Eukleides z Alexandrie (asi 300 př. n. l.) a Apollónios z Pergy (asi 200 př. n. l.), při-čemž Apollónios byl ten, kdo jim dal názvy, které používáme i dnes – elipsa, parabola a hyperbola. V matematice je kuželosečka definována jako křivka, kterou je možné získat průnikem kuželové plochy s rovinou (Obr. 1). Kuželosečky mají důležité uplatnění v astro-nomii: používají se pro popis pohybu nebeských těles pod vlivem gravitace. Dráhy těchto pohybů se nazývají oběžné dráhy (nebo trajektorie) nebeských těles.
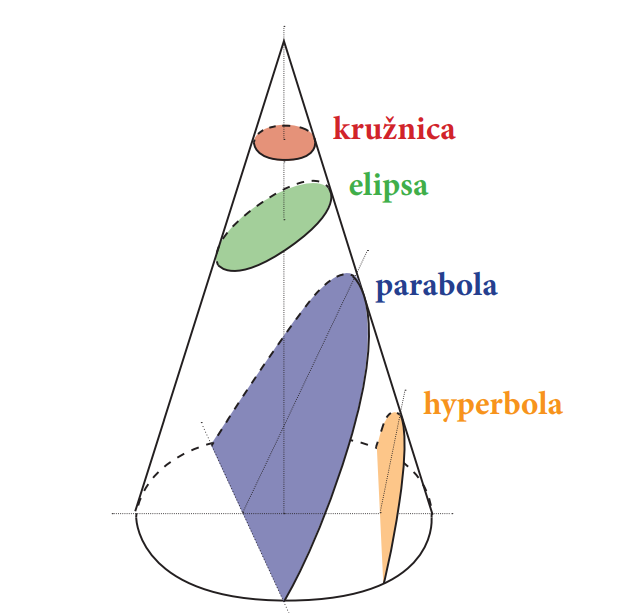
Obr 1: Kuželosečky (zdroj obrázku: http://commons.wikimedia.org/wiki/User:Magister_Mathematicae - File:Secciones_cónicas.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=18556148)
Typy kuželoseček. Parametry
Typy kuželoseček
V matematice je kuželosečka definována jako křivka, kterou je možné získat průnikem rotační kuželové plochy s rovinou, která neprochází jejím vrcholem.
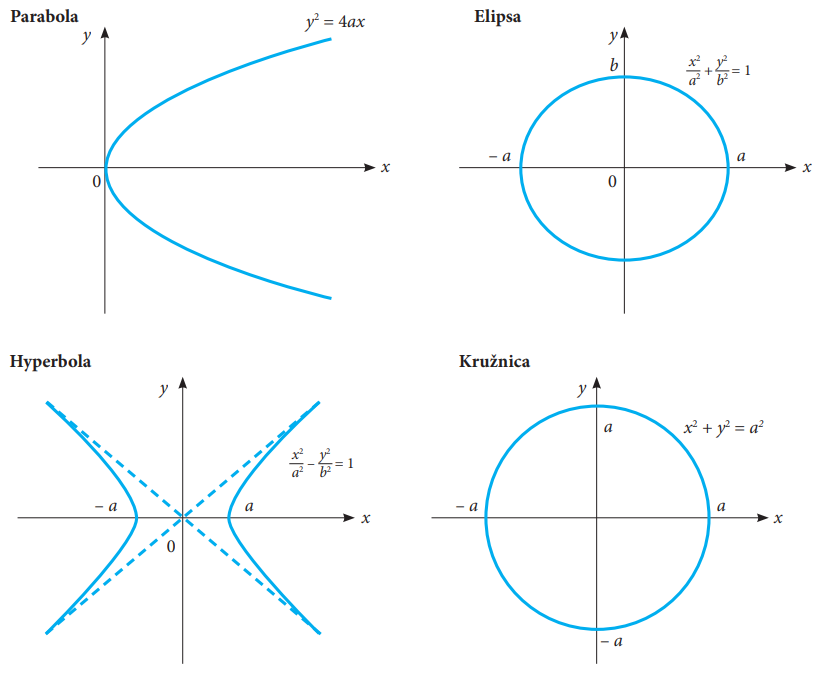
Obr. 2: Kuželosečky Zdroj: http://amsi.org.au/ESA_Senior_Years/SeniorTopic2/2a/2a_3links.html
Elipsa – uzavřená křivka se dvěma ohnisky. Elipsa má tvar zploštělého kruhu, přičemž zploštění je dáno výstředností (označuje se písmenem „e“ a hodnoty jsou od 0 do méně než 1). Elipsa se získává tak, protínáme-li rotační kužel rovinou, která svírá s osou symetrie kuželu úhel menší než 90° a větší než polovina vrcholového úhlu kuželu. Elipsa má dvě osy (hlavní a vedlejší osa), které procházejí středem a dělí elipsu vždy na dvě stejné poloviny. Půlky os se nazývají hlavní poloosa (označuje se písmenem „a“) a vedlejší poloosa (označuje se písmenem „b“). Ohniska elipsy leží na hlavních poloosách. Vzdálenost ohnisek od středu elipsy je dána součinem a a e (viz obrázek).
Kružnice – speciální případ elipsy. Získává se průnikem rotačního kužele s rovinou kolmou na osu symetrie. Výstřednost e je přesně rovna nule.
Parabola – otevřená křivka s jedním ohniskem. Získává se průnikem rotačního kužele s rovi-nou rovnoběžnou právě s jednou z povrchových přímek pláště kuželu. Výstřednost e je rovna 1.
Hyperbola – otevřená křivka, která sestává ze dvou ramen, má dvě ohniska a dvě asymptoty. Získává se průnikem rotačního kužele s rovinou, která svírá s osou symetrie kuželu úhel menší než polovina vrcholového úhlu kuželu. Výstřednost e je větší než 1.
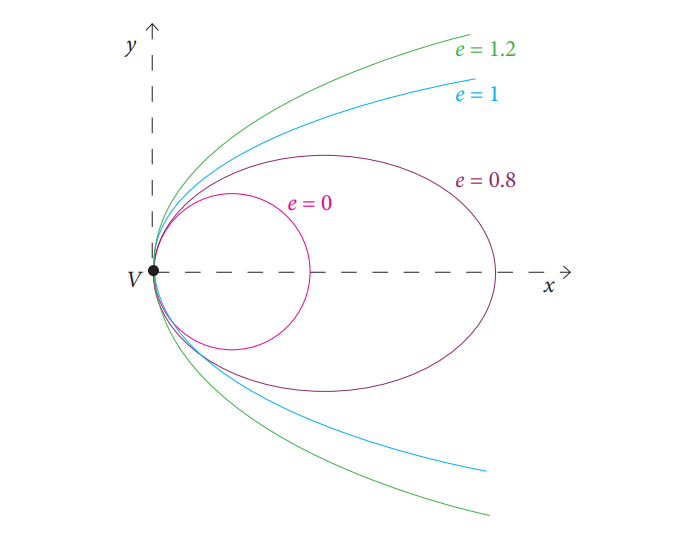
Obr. 3: Výstřednost různých kuželoseček (Zdroj: By Ag2gaeh - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=56338953 )
Výstřednost (excentricita)
Charakteristickým parametrem společným pro všechny sekce je výstřednost (e, excentricita). Lze ji chápat jako měřítko toho, jak velká je odchylka kuželosečky od kružnice. Pak pro kružnici je výstřednost nula (tj. žádná odchylka); v případě elipsy bude větší než 0, ale menší než 1; pro parabolu to bude přesně 1; pro hyperbolu to bude větší než 1 (Obr. 3).
Rovnice kuželoseček:
Výstřednost je: