Úvod
Jednotky délky, které používáme při většině fyzikálních měření, jsou vhodné pro měření předmětů, se kterými se běžně setkáváme – maximální rozměry balíku, který ještě pošta pošle, měříme v centimetrech, vzdálenost do školy a do práce v kilometrech a tak dále. Pro měření ve vesmíru pak potřebujeme odpovídající jednotky. Vzdálenost Měsíce od Země můžeme vyjádřit v kilometrech – tato vzdálenost se pohybuje přibližně mezi 363 300 a 405 500 km. Vzdálenost Slunce už ale vychází ve stovkách milionů kilometrů a vzdálenosti nejbližších hvězd by byla v bilionech kilometrů! Proto se v astronomii zavádějí takové jednotky délky, které jsou pro měření vesmírných vzdáleností vhodné.
Měření vzdáleností ve vesmíru
Astronomická jednotka
Astronomická jednotka (1 au) je definována jako střední vzdálenost středů Země a Slunce. Jedna astronomická jednotka je přibližně 150 milionů kilometrů. Podle definice Mezinárodní astronomické unie se astronomická jednotka chápe jako poloměr ničím nerušené kruhové dráhy, po které oběhne těleso o zanedbatelné hmotnosti kolem Slunce úhlovou rychlostí 0,017202 09895 radiánů za den. Její v současnosti nejpřesnější hodnota je stanovena resolucí Mezinárodní astronomické unie z r. 2009 jako 1 au = (149 597 870,700 ± 0,003) km.
Světelný rok
Světelný rok je vzdálenost, kterou urazí světlo za jeden Juliánský rok ve vakuu:
1 ly = 299 792 456 m · s–1 · 365,25 dnů · 24 hodín · 60 minut · 60 sekund = 9,461 · 1 012 km.
Paralaxa
Paralaxa je úhel, pod kterým z hvězdy vidíme nějakou definovanou délku, např. paralaxa rovníková je úhel, pod kterým bychom viděli průměr Země. Paralaxa roční p je úhel, pod kterým bychom z dané vzdálenosti viděli délku 1 au (viz obr. 1).
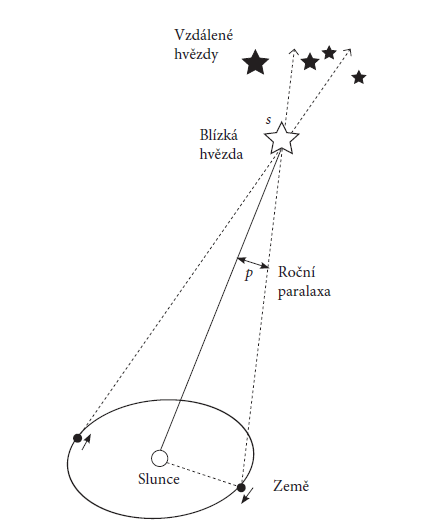
Obr. 1: Roční paralaxa
Parsek
Z astronomické jednotky vychází jednotka parsek (1 pc, někdy také parsec, z paralactic second, česky paralaktická vteřina). Jde o vzdálenost, pod kterou je vidět jedna astronomická jednotka pod úhlem jedné obloukové vteřina.
K odvození délky parseku:
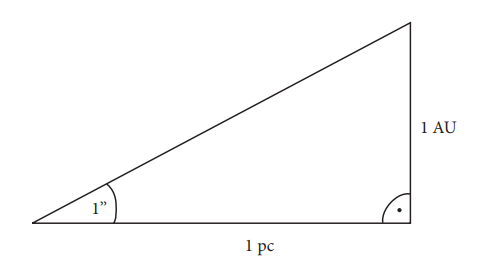
Obr. 2: Odvození délky parseku
Můžeme zapsat, že:
Jeden parsek je asi 3,2 ly.
Pokud známe roční paralaxu pmax hvězdy (změřenou podle obr. 1), její vzdálenost r určíme jako
kde r i pmax jsou ve složených závorkách, protože taková rovnice nesedí rozměrově; ve jmenovateli není funkce tangens, protože pokud budeme pmax dosazovat v radiánech, tak pro takto malé úhly je hodnota tangenty rovna přímo úhlu v radiánech a není potřeba do toho plést trigonometrické funkce..