Kepler´s laws

Kepler´s first law:

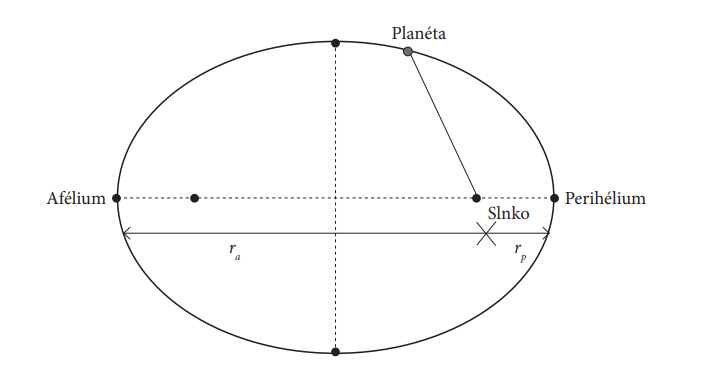
The planets move around the Sun in elliptical orbits slightly different from the circles, having the Sun as one of the foci.

It follows from Kepler's 1st law that planets move along planar closed curves. Fig. 2 depicts a specific trajectory of the planet with the Sun in focus. The point of the ellipse closest to the Sun is called the perihelion and the farthest point of the Sun aphelion. The distances from the focus are marked r_p and r_a respectively. Fig. 2 represents the radius vector of the planet (the line joining the planet and the Sun). Fig. 2 shows:

Fig. 2 Planet´s orbit around the Sun

Kepler´s second law:

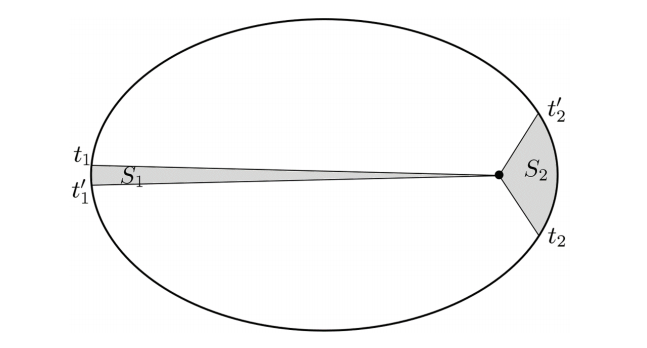
A radius vector joining any planet to the Sun sweeps out equal areas in equal lengths of time.

The meaning of Kepler's 2nd law is described in Fig. 3. Two time intervals , are recorded, which correspond to the areas described by the vectors and . respectively. It follows from Kepler's 2nd law that if , then .

Fig. 3 The interpretation of the 2nd Kepler's law

Kepler´s third law:

If we denote T1 , T2 as the orbital periods of the two planets orbiting the Sun and a1 , a2 as the lengths of the semi major axes of the ellipses, it applies

which we can read as

The ratio of the square of an object's orbital period with the cube of the semi major axis of its orbit is the same for all objects orbiting the same primary.

In the solar system, it makes natural sense for the orbital periods to be calculated in years and the semi major axes in astronomical units (abbreviated as "au", i.e. astronomical unit). For the Earth: au, = 1 year.

Note: The attentive reader might notice that this wording of the law is functional for any (physically justified) units. In other words, we can calculate the period in years, as well as in seconds or hours, the relation will still be valid. A similar reasoning applies to the semi major axis. The semi major axis can be calculated in astronomical units, as well as in meters or kilometres and the like.

Let's look at an example:

The share of periods did not depend on the units in which we calculated, because the conversion factor of 24 · 3 600 was reduced in a fraction.

Let's take our reasoning even further and show that it is possible to work even in dimensionless quantities. Let us define the (dimensionless) relative distance aʹ and the relative period Tʹ, which say how much is the distance, resp. period greater than a, resp. T:

where are semi major axis and period of the Earth.

If a = 1,5 au, then aʹ = 1,5 and so on.

Training Programme

Presentation 1

Presentation 2