- Practical exercise 1 AROUND THE SUN
- Practical exercise 2 THE MOON IN THE DISTANCE…HOW FAR??
- Practical exercise 3 THE NEIGHBOR ALSO LIKES IT
- Practical exercise 4 ALIEN VS. EARTHLING
- Practical exercise 5 GAS GIANT JUPITER
- Practical exercise 6 MARS! ...WHERE?
- Practical exercise 7 FLIGHT TO MARS ALONG HALF ELLIPSE
- Practical exercise 8 GEOSTATIONARY SATELLITE
- Practical exercise 9 CATASTROPHE ON THE SUN
- Practical exercise 10 LIGHT AS... SUPERMASSIVE BLACKHOLE!
Practical exercise 10: LIGHT AS... SUPERMASSIVE BLACKHOLE!
This task will be about estimating the mass of the supermassive black hole Sag A *, which is located in the centre of the Galaxy8. For many years, astronomers have observed the star S2 orbiting SGR A *. As the star orbits the black hole, it changes its apparent position against the starry background. The successive position of the star is recorded in the graph in the figure 10 below.
a) Using the graph and the 3rd Kepler's law, estimate the mass of Sgr A *. You know that the star S2 is 25,900 light years distant from the Earth and the orbital period of the star is 16 years. To simplify the task, consider that the orbital plane is perpendicular to the plane of observation (i.e. the inclination of the orbital plane to the direction of observation (inclination) is 90°).
b) What is the value of the mass of the supermassive black hole if the true inclination is i = 133°?
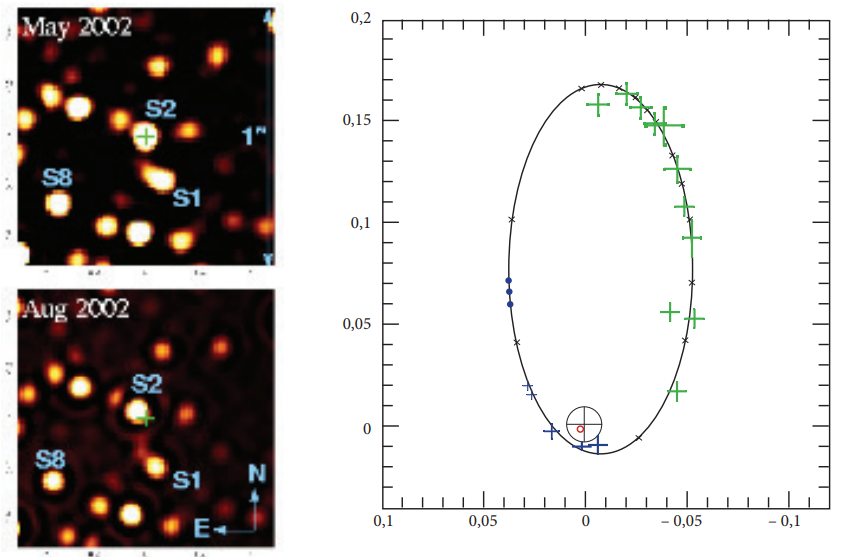
Fig. 10: https://www.astro.uni koeln.de/node/236, cit.05.07.2018
Solution:
a) We estimate the angular size of the semi major axis as (we measure
from the graph). The distance of S2 from the Earth is l = 25 900 light years = 25 900 ∙ 3 ∙
365,25 ∙ 24 ∙ 3 600 m
. It is easy to think that
, thus
. We substitute into the 3rd Kepler's law
, so the mass of the supermassive black hole is approximately
.
b) If the orbital plane is not perpendicular to the direction of observation, i.e. , we observe the projection of the orbit in the direction of observation. If the slope is
, the actual value of the semi major axis is
.From the 3rd Kepler's law we then get:
, so the mass of the supermassive black hole is approximately
.