Practical exercise 3: ORBITS. ORBITAL ELEMENTS
Aim:
To clarify and illustrate the meaning of orbits and their basic parameters and demonstrate how the orbits change depending on their parameters.
Preparatory questions:
Q: What form (conic section) are the orbits of the Solar system planets?
A: Ellipses.
Q: What form (conic section) are the orbits of the Solar system comets?
A: Ellipses.
Q: What is the difference between the orbits of the planets and the orbits of the comets?
A: Their eccentricities. They are significantly greater for comets, i.e. the orbits are more elongated.
Q: What form (conic section) are the orbits of the planets around other stars?
A: Ellipses.
Q: Are there orbits of Solar system bodies that do NOT lie in the plane of the ecliptic? If yes, which ones?
A: In practice, all orbits, besides that of Earth. Even when very small, the inclinations are present.
Q: Give some examples of orbits with large inclinations.
A: Pluto, Eris, a number of other dwarf planets and comets.
Necessary materials:
- thick cardboard,
- cork board, or other surface that you can put a push pin into,
- graph paper (A4),
- push pins,
- of thread or string (one of about 40 - 45 cm),
- pens or pencils in 4 colours,
- ruler, triangle.
1. Draw the orbits.
Instructions for the teacher:
Varying the distance between the foci and the length of the thread the students have to draw several different orbits (in different colours) and determine/compare their major axes and eccentricities.
Instructions for the students:
1.1 Secure the graph paper on top of the cork board.
1.2 Stick one pin in the centre of the paper sheet and mark with C.
1.3. Cut a thread of length 17 cm and make a loop. Make a loop of the other part of the thread as well.
1.4. At distance 2.5 cm left and right of point C stick two more pins and mark them with F1 (the pin on the right) and F2 (the one on the left).
1.5. Loop the longer thread around F1 and F2 and draw an ellipse.
1.6. Loop the shorter thread around F1 and F2 and draw another ellipse with another colour pen/pencil.
1.7. Move the pins 1cm more away from C. Use the longer thread to draw a third ellipse (different colour), and the shorter thread - for a fourth ellipse (using a fourth colour).
1.8. Compare the ellipses. Which of their parameters are different?
1.9. Calculate the eccentricity of each ellipse (Use e = c/a, where c is the distance from either focus to the centre, and а is the semi-major axis. Compare them.
1.10. Let us assume that these ellipses are orbits of some bodies from the Solar system and the Sun itself is in focus F1. On one of the orbits, mark the points of perihelion and aphelion of the body.
2. On the figure below are shown the 8 planets of the Solar system and Pluto. Let us assume that the orbits of the planets all lie in the plane of the ecliptic. What can you tell about Pluto’s orbit - is it lying in the same plane? What is the name of the orbital element that reflects the position of the orbit regarding the ecliptic? Can you draw/show it for Pluto’s orbit?
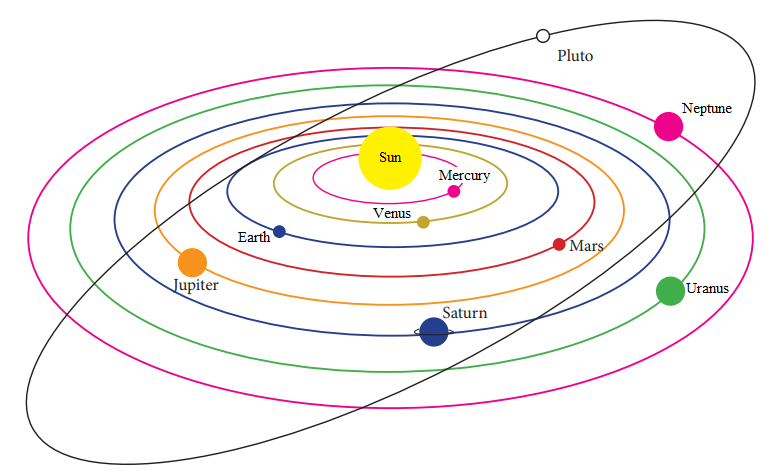
(source: http://www.rfcafe.com/references/general/solar-system.htm)
Summary questions:
Q: Which orbital element determines how far away a planet is from the Sun? How?
A: The semi-major axis (a). The larger a is, the more distant the planet is.
Q: Which orbital parameter determins how elongated they are? How?
A: Eccentricity. The larger it is, the more elongated the orbit is.
Q: What is the inclination of Earth’s orbit?
A: Zero.