- Practical exercise 1 AROUND THE SUN
- Practical exercise 2 THE MOON IN THE DISTANCE…HOW FAR??
- Practical exercise 3 THE NEIGHBOR ALSO LIKES IT
- Practical exercise 4 ALIEN VS. EARTHLING
- Practical exercise 5 GAS GIANT JUPITER
- Practical exercise 6 MARS! ...WHERE?
- Practical exercise 7 FLIGHT TO MARS ALONG HALF ELLIPSE
- Practical exercise 8 GEOSTATIONARY SATELLITE
- Practical exercise 9 CATASTROPHE ON THE SUN
- Practical exercise 10 LIGHT AS... SUPERMASSIVE BLACKHOLE!
Practical exercise 4: ALIEN VS. EARTHLING
A comet orbits around the Sun, where its perihelion is at a distance of and its aphelion is at a distance of
see FIG. 2.
Specify:
a) main and minor axes, distance and numerical eccentricity of the ellipse,
b) the period of the comet,
c) how many times the comet in perihelion has a higher speed than in aphelion.
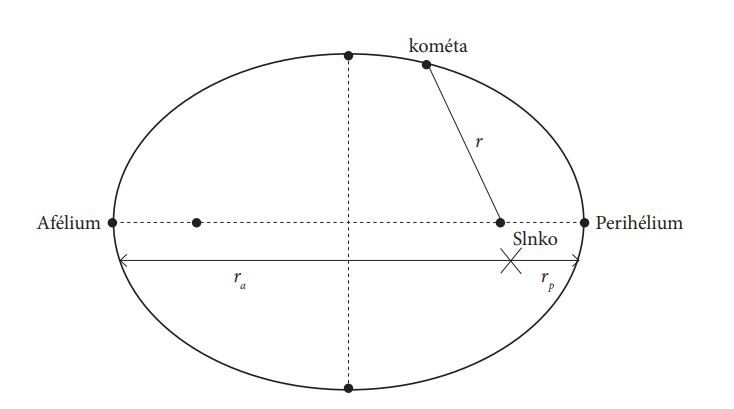
Fig. 2 Schematic sketch of the comet's trajectory
Solution:
From the geometry of the ellipse we get: ,
,
.
. The comet's trajectory is expectedly very eccentric.
b) We write the 3rd Kepler's law in the form where we substitute
with a numerical value in astronomical units, for
ʹ a numerical value in years and for
multiples of the mass of the Sun. Because we are solving the orbit of a comet in the solar system,
. automatically applies. Thus,
applies as well. But as we know, in a given formulation of the law, all quantities are dimensionless. The numerical value
represents how many times the period is greater than the period of the Earth's rotation around the Sun (i.e. how many times the period is greater than one year). The period is thus
.
It is possible to use another (but of course equivalent) notation of the 3rd Kepler's law. If we work in the SI system, we write the 3rd Kepler's law as .
We know the mass of the Sun, the gravitational constant has the value
and the semi
major axis is .
From the 3rd Kepler's law we express the period: years.
c) From the 2nd Kepler's law it follows .