Practical exercise 6: MARS! ...WHERE?

The semi major axis of Mars´ trajectory is the semi major axis of the Earth's trajectory is . Assume that the planets orbit in the same plane in the same direction.

a) Determine the orbital period of Mars around the Sun.

b) Determine the angular velocity of Mars around the Sun, as well as the angular velocity of the Earth.

c) As the planets move in the same direction, subtract the angular velocities from each other to obtain the mutual angular velocity (see Figures 4 and 5).

d) Determine the so called synodic orbital period, which is the period during which the Earth, Mars and the Sun get into the same order.

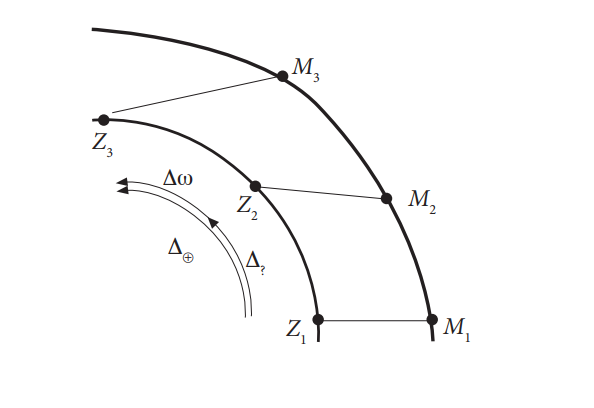
Fig. 4 Angular velocity of Mars around the Sun is smaller than the Earth´s one

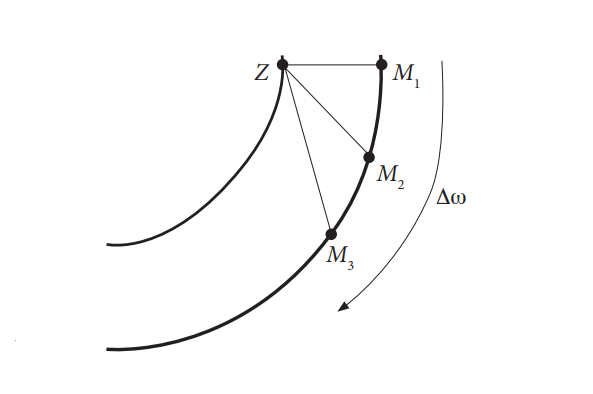
Fig. 5 From the earthlings´ point of view, Mars is moving at angular velocity Δω

Riešenie:

a) We use the 3rd Kepler's law in the same way as in the tasks IV and V: so the orbital period is T = 1,87 years.

b) Angular velocity is defined as "the angle described by radius vector per unit of time". Since in one orbital period T the radius vector describes an angle of 360°,average angular velocity is equal to . Because we assume that the trajectories of the Earth and Mars are exactly circular, it is also an instantaneous angular velocity that is the same at all times. The angular velocity of the Earth around the Sun is ,

Mars around the Sun .

c) The planets move in the same direction, and thus the mutual angular velocity is equal to

d) For the synodic period P the following applies: .

Most possibly, we can get the general result modification.