- Practical exercise 1 AROUND THE SUN
- Practical exercise 2 THE MOON IN THE DISTANCE…HOW FAR??
- Practical exercise 3 THE NEIGHBOR ALSO LIKES IT
- Practical exercise 4 ALIEN VS. EARTHLING
- Practical exercise 5 GAS GIANT JUPITER
- Practical exercise 6 MARS! ...WHERE?
- Practical exercise 7 FLIGHT TO MARS ALONG HALF ELLIPSE
- Practical exercise 8 GEOSTATIONARY SATELLITE
- Practical exercise 9 CATASTROPHE ON THE SUN
- Practical exercise 10 LIGHT AS... SUPERMASSIVE BLACKHOLE!
Practical exercise 9: CATASTROPHE ON THE SUN
The fourth cosmic velocity is the velocity at which the object would have to be fired against the direction of the Earth's motion in order to stop in free space and then begin to fall along the axis into the Sun, see Fig. 9. Such an object can be, for example, a container filled with bulky material which needs to be disposed of. The Sun thus serves as a kind of "incinerator". Use the 3rd Kepler's law in an appropriate way to calculate the period the container falls into the Sun.
Assistance with the task: When the container falls until the moment of collision with the Sun, it passes the axis, which can be seen as a special case of an ellipse (ellipse with a = e, b = 0).
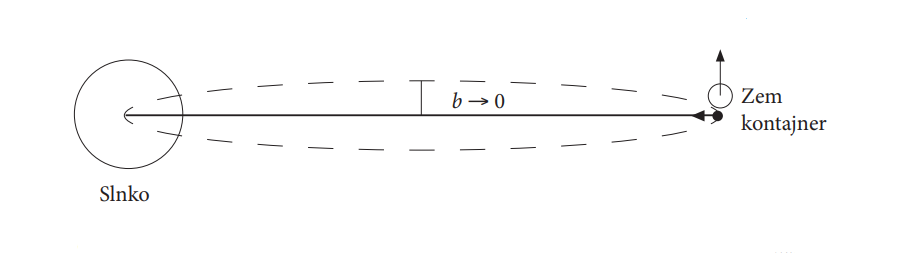
Fig. 9 The container moves along an axis that can be imagined as an ellipse with a very small semi minor axis. The beginning of the axis (right) corresponds to the point of discharge; the end of the axis (left) corresponds to the centre of the Sun. The image is not in the ratio of the actual distances, it is only illustrative.
Solution:
From the drawn picture we realize that the semi major axis of the "ellipse" is 
.
If we want to use the 3rd Kepler's law in the form
, then 
, and therefore 
.
The period is approximately 
. However, the container will not return to where it began to fall. The container burns in the Sun, so it passes only half of the "ellipse", so the time of fall corresponds to half of the calculated period: 64 days.
Note: From the picture, it might seem that the container will fly into the Sun before the period of 
and this is of course true. It is important to realize that although the dimensions of the Sun are "huge" (compared to our daily experience, for the imagination the radius of the Sun is 
), compared to the distance of the Earth the Sun they are negligible. The Sun can be considered as a material point in this approximation and the previous calculation is therefore correct.