INTRODUCTION
Conic sections are among the most ancient and long studied mathematical curves. It is thought that it was one of Alexander the Great’s teachers that first came upon them in 4th century B.C. Later, they are studies by Euclidus (around 300 B.C. ). thir study culminated around 200 B.C. with the work of Apollonius of Perga who gave them their present names - an ellipse, a hyperbola and a parabola. In mathematics, a conic section is defined as a curve obtained by the intersection of a plane and the surface of a cone. (Fig.1). In astronomy they have an important role - they are used to describe the motions of the celestial bodies under the force of gravitation. The trajectories of these motions are called orbits of the celestial bodies.
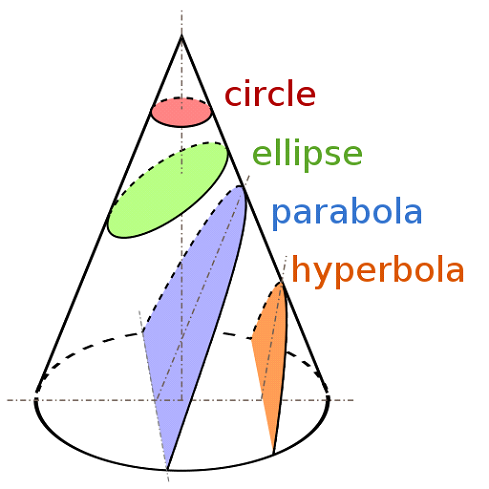
Fig. 1 conic sections. (Image from: http://commons.wikimedia.org/wiki/User:Magister_Mathematicae - File:Secciones_cónicas.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=18556148)
Types of conic sections. Parameters
In mathematics, a conic section is defined as a curve obtained by the intersection of a plane and the surface of a cone. The types of conic sections are:
- an ellipse – a closed curve with two foci. The ellipse looks like a squeezed circle, where the eccentricity (denoted by e and having value between 0 and 1) determines how oval the ellipse is. It has two axes - major and minor – which go through the centre and split the ellipse in two equal halves. The halves of the axes themselves – semi-major axis (denoted by a) and semi-minor axis (denoted by b). The foci of the ellipse lie on the semi-major axes. The distance from the centre to each focus is determined by multiplying a by e (figure).
- a circle - a special case of the ellipse. It is a product of the intersection of a right circular cone (A right circular cone is defined as a cone with a circle as its base and the apex is centered directly over the center of the circle so that the height from the base to the apex is at a right angle from the center of the circle to the apex.) with a plane perpendicular to the cone’s axis.
- a parabola - unbounded curve with one focus. It is obtained when the cutting plane is parallel to exactly one generating line of the cone.
- a hyperbola - unbounded curve with two foci. It is an intersection of the two halves of the cone with a plane which is not parallel two a generating line.
A characteristic parameter, common for all conic sections is the eccentricity (e). It can be considered as a measure of how much the conic section deviates from being circular. Then, eccentricity of a circle is zero (i.e. no deviation); for an ellipse it is greater than zero but less than 1; for a parabola it is 1; for a hyperbola it is greater than 1. (Fig. 3)
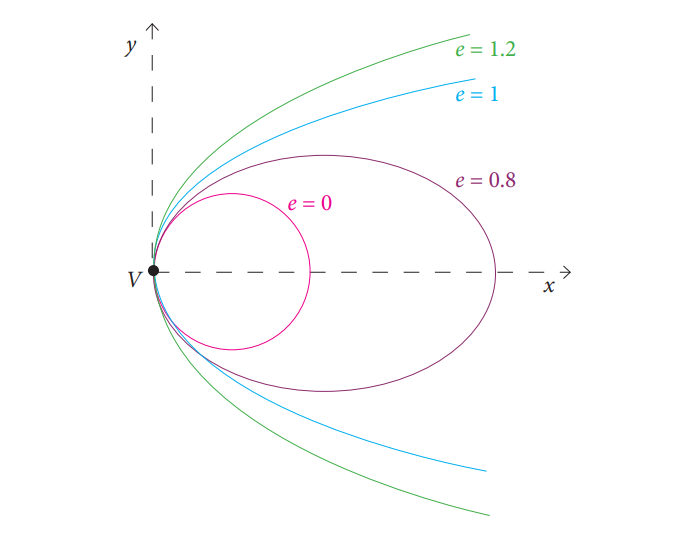
Fig. 3 Eccentricities of the conic sections(Credit: By Ag2gaeh - Own work, CC BY-SA)
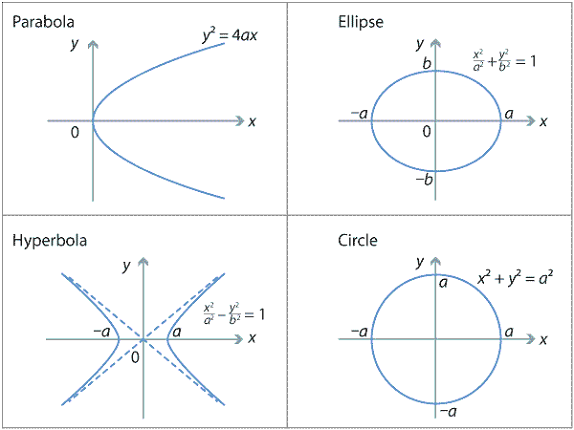
Additional information: The conic sections equations are:
The eccentricity is: