- Practical exercise 1 AROUND THE SUN
- Practical exercise 2 THE MOON IN THE DISTANCE…HOW FAR??
- Practical exercise 3 THE NEIGHBOR ALSO LIKES IT
- Practical exercise 4 ALIEN VS. EARTHLING
- Practical exercise 5 GAS GIANT JUPITER
- Practical exercise 6 MARS! ...WHERE?
- Practical exercise 7 FLIGHT TO MARS ALONG HALF ELLIPSE
- Practical exercise 8 GEOSTATIONARY SATELLITE
- Practical exercise 9 CATASTROPHE ON THE SUN
- Practical exercise 10 LIGHT AS... SUPERMASSIVE BLACKHOLE!
Practical exercise 8: GEOSTATIONARY SATELLITE
A geostationary satellite is a satellite that Earthlings see "hanging" motionless in the sky. The satellite must be in the plane of the equator and orbit along the circle in the same direction as the direction of rotation of the Earth about its axis, see Fig. 7 and 8.
a) Explain why it is not possible for the satellite to move in another plane.
b) The mass of the Earth is and rotation around the axis takes T = 24 hod. Determine how high the satellite orbits above the Earth's surface.
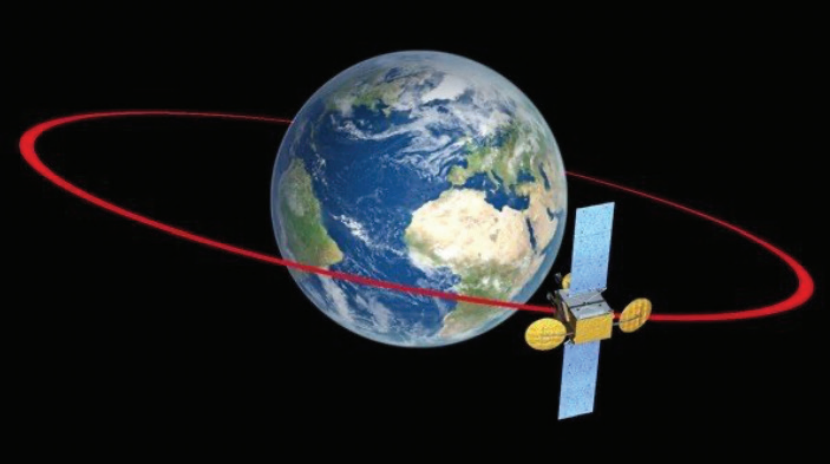
Fig. 7 https://www.esa.int/spaceinimages/Images/2009/03/Geostationary_orbit, cit. 05.07.2018
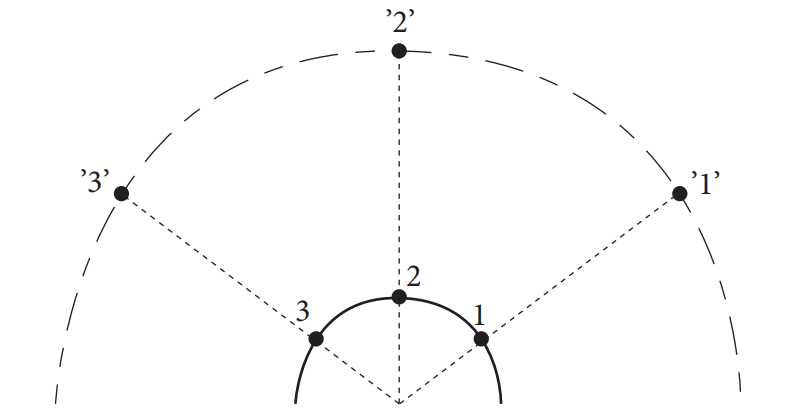
Fig. 8 From the observer's point of view, the geostationary satellite "“hangs" over one point on the Earth's surface (illustrative image)
Solution:
a) The plane of a satellite´s orbit must pass through the centre of the Earth (mass centre). If the satellite, from the point of view of an observer connected to the Earth's surface, is to always be at the same point, it must rotate in the direction of the Earth's rotation. However, this means that the plane of rotation must be perpendicular to the axis of rotation. It is then clear from the geometric idea that there is only one such plane.
b) The semi major axis (radius of a circular trajectory) is found by 3rd Kepler's law
The centre of the circular orbit of the satellite lies in the centre of the Earth (in the mass centre or focus).
The distance of the satellite above the Earth's surface is then: