INTRODUCTION
In this text we will introduce the so-called aspects, significant positions of planets in the Solar System from the perspective of the Earth. Step by step we will explain the terms conjunction, opposition, elongation, quadrature, and we will look into how to determine the distance of a planet located at one of these significant points from the Earth.
Next, we will explain how the angular size of a body is defined and how knowing this parameter and knowing the distance of the body will help us determine the actual dimensions of the body. In general, we must work with trigonometric functions for this. However, we will explain why in cases where the bodies are at a great distance from the observer, we can disregard the goniometric functions and simplify the calculation. For this purpose, we will naturally introduce very useful angular units, the so-called radians.
Distances and sizes
Typical distances in the Solar System
Mean distance the Earth – the Sun equalskm polomer Zeme je
radius of the Earth is
km. Vaable 1 shows the mean distances of the planets from the Sun and their radii in multiples of the Earth’s radii. For comparison, we also present the radius of the Sun. ahe dimensions of the Sun appear to be huge compared to other planets, but it is interesting to convert the radius of the Sun into astronomical units:
km, the radius of the Earth equals
km. aable 1 shows the mean distances of the planets from the Sun and their radii in multiples of the Earth's radii. For comparison, we also present the radius of the Sun. ahe dimensions of the Sun appear to be huge compared to other planets, but it is interesting to convert the radius of the Sun into astronomical units:
. From this it can be seen that neither the planets nor the Sun take up a large space of the Solar System.
Table 1: Mean distances of the planets in the Solar System and radii of the planets and the Sun
| Body | Distance from the Sun [au] | R/R⊕ |
| The Sun | 0 | 109 |
| Mercury | 0,39 | 0,38 |
| Venus | 0,72 | 0,95 |
| The Earth | 1,00 | 1,00 |
| Mars | 1,52 | 0,53 |
| Jupiter | 5,20 | 11,2 |
| Saturn | 9,54 | 9,45 |
| Uranus | 19,2 | 4,01 |
| Neptune | 30,07 | 3,88 |
Aspects of the planets
From the point of view of the Earth, we distinguish several significant positions of the planets, the so-called aspects which are schematically drawn in Figure 1 and their description is given below.
1. Conjunction
With the inferior planets (Mercury, Venus) we recognize the superior and inferior conjunction. ahe superior conjunction is the moment when the planet is on the opposite side of the Sun1 (the Sun is between the Earth and the inferior planet). ahe lower conjunction occurs when the planet is between the Earth and the Sun. ahe superior planet (Mars, Jupiter, Saturn, Uranus, Neptune) can only be in the superior conjunction.
If the planet is in conjunction, it rises and sets together with the Sun, it is in the daytime sky and is not observable to us.
2. Opposition
ahe moment when the superior planet is closest to the Earth, or the earth is between the planet and the Sun is called the opposition. In the time of opposition, the conditions for observing a planet are the most favourable, because the planet rises at sunset and sets at sunrise (it is thus observable throughout the night) and the planet appears to be the largest in the telescope (i.e. it has the largest angular size).
3. Elongation
Elongation is the angular distance between the inferior planet and the Sun. At the western elongation, the planet rises and sets earlier than the Sun. At the eastern elongation, the Sun rises and sets earlier than the planet. ahe greatest angular distance of the planet from the Sun is called the greatest elongation2. ahe greatest elongation of Mercury is 23°, of Venus is 47°.
4. Quadrature
Quadrature is the moment when the angle of the Sun - the Earth - the superior planet is right. Only superior planets can be in quadrature.
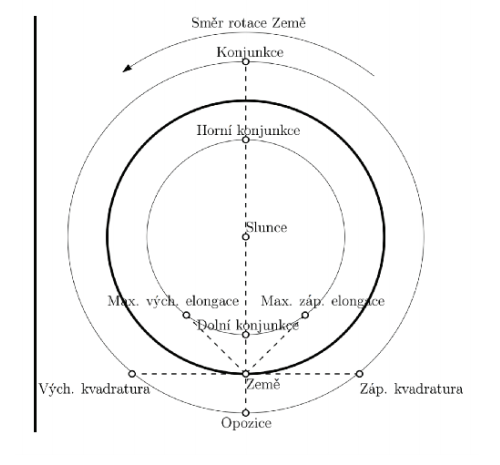
Figure 1: Diagram of possible planet configurations
Angular sizes of objects
It is natural that if objects are at a great distance from us, they seem to be smaller than if they were in our immediate vicinity. Nevertheless, their physical dimensions do not change. In order to be able to describe this fact qualitatively, we introduce the quantity of angular size θ, the meaning of which is described in Figure 2. ahe figure gives us a clear idea of how to calculate the angular size:
ahe angle θ is calculated as follows: . Just to give an idea, for the Sun with the radius θ we will calculate as follows:
.Just to give an idea, for the Sun with the radius
, with the distance of θ, we will calculate as follows:
. Just to give an idea, for the Sun with the radius
, with the distance of
the angular size will be θ, we will calculate as follows:
. Just to give an idea, for the Sun with the radius
with the distance of
the angular size will be θ☉ ≐ 32'. It’s probably no surprise that the angular sizes of the planets in the Solar System are in the order of ones to tens of seconds of arc. Next we will show how to simplify the relationship for calculating the angular size if it is small. ao do this, it will be necessary to introduce “new” units of plane angle, the so-called radians.
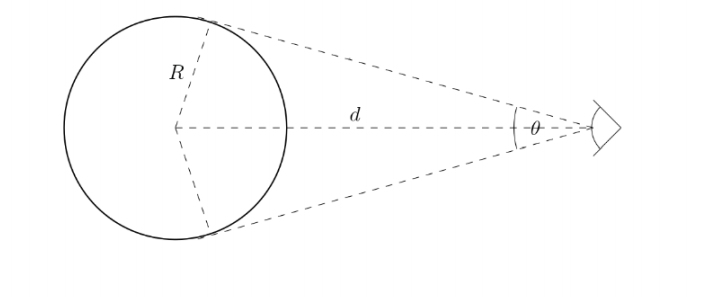
Figure 2: In relation to the definition of angular size
Radians
Radians are the most naturally defined units of the plane angle. Imagine concentric circles as in Figure 3. ahe angle θ is defined as the ratio of the length of the corresponding arc to the radius of the circle. From Figure 3 it can be seen that the angle does not depend on the specific length of the arc or radius: θ is defined as the ratio of the length of the corresponding arc to the radius of the circle. From Figure 3 it can be seen that the angle does not depend on the specific length of the arc or radius:
3 , only from their ratio, which is natural and correct. We already know how to define an angle, but we still don't know what a “radian” is.
From how we defined an angle (the length of the arc divided by the radius) it would seem that the angle has no dimension, or the unit of an angle is a “unit”. And that’s exactly what is called a radian! For the dimension of an angle we could also write:. ahere is a large number of dimensionless quantities. By writing “rad” to numbers, we point out that the number corresponds to the size of the angle. As the radius of the circle is
, the full angle is
the full angle is
. Indeed,,
, the full angle is
. Indeed,
. ahe second last equality gives the conversion relationship between radians and degrees:
, the full angle is
. Indeed,
.ahe second last equality gives the conversion relationship between radians and degrees:
,the full angle is
. Indeed,
.ahe second last equality gives the conversion relationship between radians and degrees:
.
Next, we should realise that the smaller the angle θ, the smaller the arc (from the length θ, the more the arc (from the length Δs) will be similar to a line segment. We will use this fact in the next paragraph.
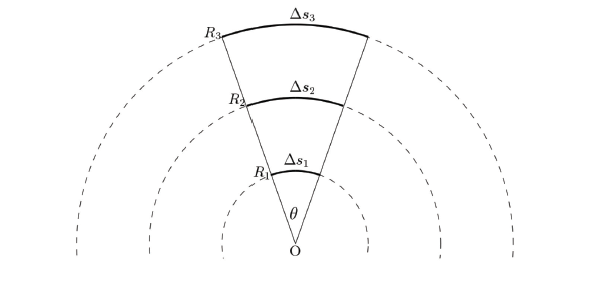
Figure 3: In relation to the introduction of radians
Angular size for a second time
Now imagine that the size of a spherical object is significantly smaller than its distance from us. As we indicated above, for large distances the (sufficiently small) length of an arc can be well estimated by a line segment and vice versa. In this case, it is possible to write for the angular size of an object (in radians):
Of course, the relation must give the same results for small angular sizes for which it is derived as for the previously derived relation, i. e. , whilst the angle is
, whilst the angle θ is calculated in radians (the calculator can calculate the tangent in degrees as well as in radians).
Resources and recommended literature:
[1] Mikulčák J., Macháček M., Zemánek F.: Matematické,fyzikální a chemické tabulky a vzorce pro SŠ, Prometheus, Praha, 2003
[2] Široký J., Široká M.: Základy astronomie v příkladech, SPN, Praha, 1966, online odkaz: http://physics.ujep.cz/~zmoravec/astronomie/siroky/siroky.html, cit. 8.7.2018