- Practical Exercise 1 RADIANS OR DEGREES?
- Practical Exercise 2 MARS IN OPPOSITION AND QUADRATURE
- Practical Exercise 3 MEASURING MERCURY AND VENUS
- Practical Exercise 4 “MERCUAN”
- Practical Exercise 5 THE EARTH FROM MARS
- Practical Exercise 6 HOW BIG IS THE MOON?
- Practical Exercise 7 THE MOON AGAIN
- Practical Exercise 8 PARAMETERS OF PLANET TRAJECTORIES
- Practical Exercise 9 LIKE FROM ANOTHER PLANET...
- Practical Exercise 10 FEET FIRMLY ON THE EARTH...
- Practical Exercise 11 GREEK, HOW BIG IS THE EARTH?
- Practical Exercise 12 THE MOON IN ACTION FOR THE THIRD TIME
Practical Exercise 10: FEET FIRMLY ON THE EARTH...
A mountain climber climbed the highest mountain in the world, Mount Everest, with an altitude of 8848 m above sea level. m. If we considered the Earth as a perfect sphere, except for the place where Mount Everest lies, how much of the Earth’s surface would the mountain climber see? ahe radius of the Earth equals R⊕ = 6 378 km.
Answer:
According to the picture: , i. e.
, i. e.
, i. e. approximately
, teda
, i. e. approximately
. It is also clear from the picture:
, i. e.
, i. e. approximately
.
It is also clear from the picture: , therefore
, therefore
, i. e.
, i. e. approximately
.It is also clear from the picture:
, therefore
.
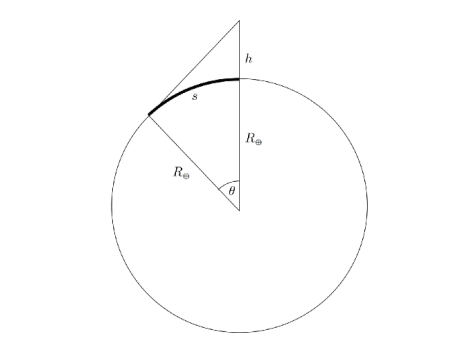
Figure 5 An observer on Mount Everest with the height ℎ can see into the distance ℎ can see into the distance