- Practical Exercise 1 RADIANS OR DEGREES?
- Practical Exercise 2 MARS IN OPPOSITION AND QUADRATURE
- Practical Exercise 3 MEASURING MERCURY AND VENUS
- Practical Exercise 4 “MERCUAN”
- Practical Exercise 5 THE EARTH FROM MARS
- Practical Exercise 6 HOW BIG IS THE MOON?
- Practical Exercise 7 THE MOON AGAIN
- Practical Exercise 8 PARAMETERS OF PLANET TRAJECTORIES
- Practical Exercise 9 LIKE FROM ANOTHER PLANET...
- Practical Exercise 10 FEET FIRMLY ON THE EARTH...
- Practical Exercise 11 GREEK, HOW BIG IS THE EARTH?
- Practical Exercise 12 THE MOON IN ACTION FOR THE THIRD TIME
Practical Exercise 6: HOW BIG IS THE MOON?
a) Mean distance the Earth – the Sun equals d = 1 au = 1,496 ⋅ 108 km, radius of the Sun is d = 1 au = 1,496 ⋅ 108 km, radius of the Sun is R☉ = 6,955 ⋅ 105 km. Find the angular size of the Sun for an observer on the Earth.
b) Based on the knowledge of the mass of the Earth M⊕ = 5,97 ⋅ 1024 kg and the time of the orbit of the Moon around the Earth M⊕ = 5,97 ⋅ 1024 kg and the time of the orbit of the Moon around the Earth T = 27,3 days, estimate from the 3rd Kepler’s law the distance of the Moon from the Earth. When estimating the distance, do not take the weight of the Moon into consideration.
c) Since you know that there are both partial and total solar eclipses, estimate the actual dimensions of the Moon. ahe phenomenon is illustrated in Figure 2.

Figure 2
https://apod.nasa.gov/apod/ap160831.html, cit. 5.8.2018

Figure 3
https://www.nasa.gov/multimedia/imagegallery/image_feature_1249.html, cit. 5.8.2018
What would be the angular size of the Earth for an astronaut on the Moon if the moon moved on a precisely circular orbit? How much of the surface of the Earth can the astronaut see (see Figures 3 and 4)? Write the result as a percentage. ahe radius of the Earth equals R⊕ = 6 378 km.
Clue: ahe part of the Earth’s surface that the observer can see corresponds to the surface of the spherical apex. ahe area of the spherical apex (without base) is , where
, where R is a radius of the sphere and
, where R is the radius of the sphere and v is the height of the spherical sector, see Figure 4.
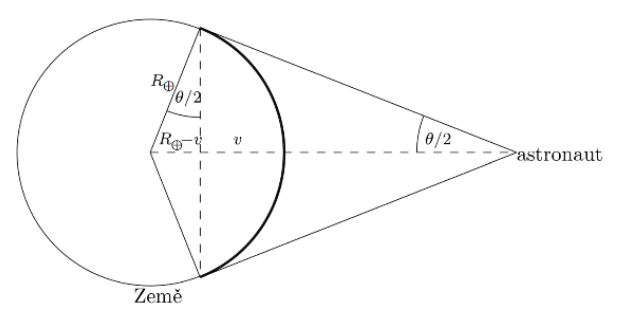
Figure 4 Illustration of an astronaut’s view of the Earth
Answer:
a) We start from the approximate relation for angular size: .
We could also start from the exact relation
We could also start from the exact relation
or
.
We could also start from the exact relation tg . The results are, of course, the same, see Practical Exercise I.
b) We start from the 3rd Kepler’s law: .
c) As there are partial and total solar eclipses, the angular size of the Moon is comparable to the angular size of the Sun, i. e. . We determine the radius of the Moon from the relation:
. We determine the radius of the Moon from the relation:
. The actual radius of the Moon is 1 737 km, so our result corresponds well with reality.
d) We start from the approximate relation for angular size: .
Based on Figure 2 it is obvious that: . Based on Figure 2 it is obvious that:
. Based on Figure 2 it is obvious that:
.
We can either calculate the height of the spherical apex directly from the given values, or from the calculated value of the angular size of the Earth. We will insert values into the auxiliary formula for the area of the spherical apex . Based on Figure 2 it is obvious that:
.
We can either calculate the height of the spherical apex directly from the given values, or from the calculated value of the angular size of the Earth. We will insert values into the auxiliary formula for the area of the spherical apex
. The formula for the area of a sphere is
.
Based on Figure 2 it is obvious that:
.
We can either calculate the height of the spherical apex directly from the given values, or from the calculated value of the angular size of the Earth. We will insert values into the auxiliary formula for the area of the spherical apex
. The formula for the area of a sphere is
, therefore the ratio of the area of the spherical apex to the whole sphere is:
. Based on Figure 2 it is obvious that:
.
We can either calculate the height of the spherical apex directly from the given values, or from the calculated value of the angular size of the Earth. We will insert values into the auxiliary formula for the area of the spherical apex.
. ahe formula for the area of a sphere is
, therefore the ratio of the area of the spherical apex to the whole sphere is:
.ahe astronaut can see almost one entire side of the Earth. From the last equation it is clear that the farther the astronaut is from the Earth (the distance is given by the main half-axis, because it corresponds to the radius of the circular orbit), the more the term
. Based on Figure 2 it is obvious that:
.
. ahe formula for the area of a sphere is
, therefore the ratio of the area of the spherical apex to the whole sphere is:
.
ahe astronaut can see almost one entire side of the Earth. From the last equation it is clear that the farther the astronaut is from the Earth (the distance is given by the main half-axis, because it corresponds to the radius of the circular orbit), the more the term is closer to zero and the astronaut can see a larger part of the Earth, but at most
. Based on Figure 2 it is obvious that:
. We can either calculate the height of the spherical apex directly from the given values, or from the calculated value of the angular size of the Earth. We will insert values into the auxiliary formula for the area of the spherical apex
. ahe formula for the area of a sphere is
, therefore the ratio of the area of the spherical apex to the whole sphere is:
. ahe astronaut can see almost one entire side of the Earth. From the last equation it is clear that the farther the astronaut is from the Earth (the distance is given by the main half-axis, because it corresponds to the radius of the circular orbit), the more the term
is closer to zero and the astronaut can see a larger part of the Earth, but at most 50 %. If, on the other hand, the astronaut is just above the Earth’s surface, the term
. Based on Figure 2 it is obvious that:
. We can either calculate the height of the spherical apex directly from the given values, or from the calculated value of the angular size of the Earth. We will insert values into the auxiliary formula for the area of the spherical apex
. The formula for the area of a sphere is
,therefore the ratio of the area of the spherical apex to the whole sphere is:
. The astronaut can see almost one entire side of the Earth. From the last equation it is clear that the farther the astronaut is from the Earth (the distance is given by the main half-axis, because it corresponds to the radius of the circular orbit), the more the term
is closer to zero and the astronaut can see a larger part of the Earth, but at most 50 %. If, on the other hand, the astronaut is just above the Earth’s surface, the term
will be close to 1 and the ratio
. Based on Figure 2 it is obvious that:
. We can either calculate the height of the spherical apex directly from the given values, or from the calculated value of the angular size of the Earth. We will insert values into the auxiliary formula for the area of the spherical apex
. The formula for the area of a sphere is
, therefore the ratio of the area of the spherical apex to the whole sphere is:
. The astronaut can see almost one entire side of the Earth. From the last equation it is clear that the farther the astronaut is from the Earth (the distance is given by the main half-axis, because it corresponds to the radius of the circular orbit), the more the term
is closer to zero and the astronaut can see a larger part of the Earth, but at most 50 %. If, on the other hand, the astronaut is just above the Earth’s surface, the term
will be close to 1 and the ratio
will be almost zero.