- Practical Exercise 1 RADIANS OR DEGREES?
- Practical Exercise 2 MARS IN OPPOSITION AND QUADRATURE
- Practical Exercise 3 MEASURING MERCURY AND VENUS
- Practical Exercise 4 “MERCUAN”
- Practical Exercise 5 THE EARTH FROM MARS
- Practical Exercise 6 HOW BIG IS THE MOON?
- Practical Exercise 7 THE MOON AGAIN
- Practical Exercise 8 PARAMETERS OF PLANET TRAJECTORIES
- Practical Exercise 9 LIKE FROM ANOTHER PLANET...
- Practical Exercise 10 FEET FIRMLY ON THE EARTH...
- Practical Exercise 11 GREEK, HOW BIG IS THE EARTH?
- Practical Exercise 12 THE MOON IN ACTION FOR THE THIRD TIME
Practical Exercise 12: THE MOON IN ACTION FOR THE THIRD TIME
a) Figure 6 shows the total Lunar eclipse. With the help of Figure 6 and times, estimate how many times the radius of the Earth’s shadow is larger than the radius of the Moon.
b) If the angular magnitude of the Sun is θ☉ = 32', the radius of the Earth equals R⊕ = 6 378 km and the radius of the circular orbit is θ☉ =32‘, the radius of the Earth equals R⊕ = 6 378 km and the radius of the circular orbit is a2 = 384 400 km, calculate with the help of the result in point a) the radius of the Moon. Figure 7 can help.
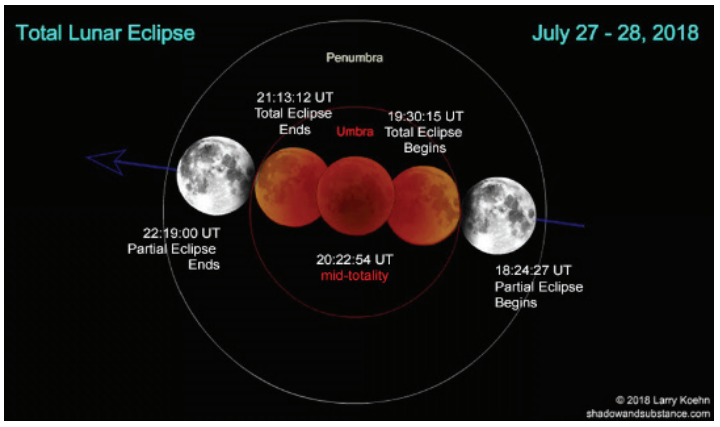
Figure 6 Lunar Eclipse
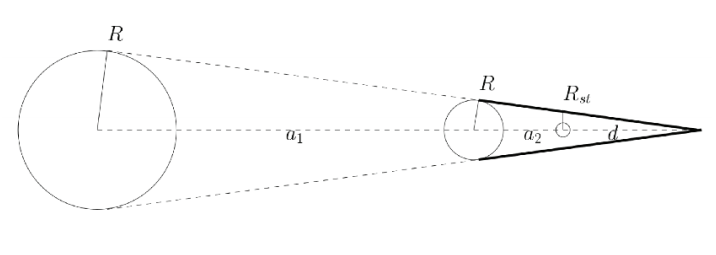
Figure 7 Lunar Eclipse - situation analysis
Answer:
a) From the times shown in the picture, it is clear that it took the Moon about 1 hour and 6 minutes to enter the Earth’s shadow. It then remained in this shadow for approximately 2 hours and 49 minutes. The ratio of these times then corresponds to the ratio of the diameter of the Earth’s shadow and the radius of the Moon:
As the Moon’s passage through the Earth’s shadow is not exactly central, the ratio will actually be a little greater.
b) The sketch shows the following: .
Since , it is possible to write the left side of the first equation as
, it is possible to write the left side of the first equation as
, which is equal to
, it is possible to write the left side of the first equation as
, which is equal to
. From the first equation we can simply express
,it is possible to write the left side of the first equation as
, which is equal to
. From the first equation we can easily express
. From the second equation we get
it is possible to write the left side of the first equation as
, which is equal to
. From the first equation we can easily express
. From the second equation we get
.
We get the radius of the Moon as follows: , it is possible to write the left side of the first equation as
, which is equal to
. From the first equation we can easily express
. From the second equation we get
. We get the radius of the Moon as follows:
. The actual radius of the Moon is 1737 km, so the result gives a reasonable estimate.