ВЪВЕДЕНИЕ
Коничните сечения са едни от най-древните и продължително изучавани геометрични криви. Предполага се, че те първоначално са открити от Менехм (един от учителите на Александър Македонски) през 4 век пр. не. е. По-късно те са изучавани от Евклид (около 300 г пр. н. е.) и Аполоний Пергски (около 200 г. пр. н.е.), като Аполоний е този, който дава имената им, които ползваме и до днес – елипса, парабола и хипербола. В математиката конично сечение се дефинира като крива, която може да се получи от сечението на повърхнината на конус с равнина (Фиг.1). Коничните сечения имат важно приложение и в астрономията: те се използват за описване на движението на небесните тела под въздействието на гравитацията. Траекториите на тези движения се наричат орбити на небесните тела.
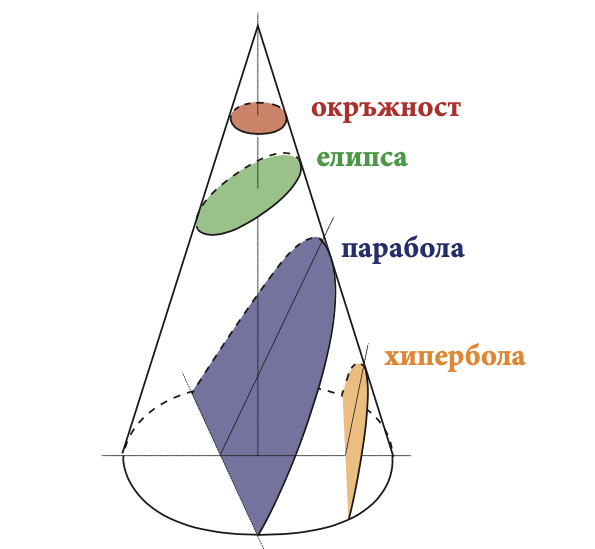
Фиг. 1: Конични сечения (Източник: http://commons.wikimedia.org/wiki/User:Magister_Mathematicae - File:Secciones_cónicas.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=18556148)
Съдържание на темата
В частта за учителя към тази тема първо ще опишем видовете конични сечения и техните параметри, след което ще разгледаме приложението им в астрономията за описване на движението на небесните тела под действието на гравитацията. Ще се спрем на орбитите на телата от Слънчевата система. Накрая ще опишем елементите на една орбита. В частта с практически упражнения за ученика ще предложим няколко интересни практически упражнения и въпроси, които имат за цел да илюстрират материала и да спомогнат за неговото по-добро усвояване.
Видове конични сечения. Параметри
Видове конични сечения
В математиката конично сечение се дефинира като крива (от втора степен), която може да се получи от сечението на повърхнината на конус с равнина. Видовете конични сечения са:
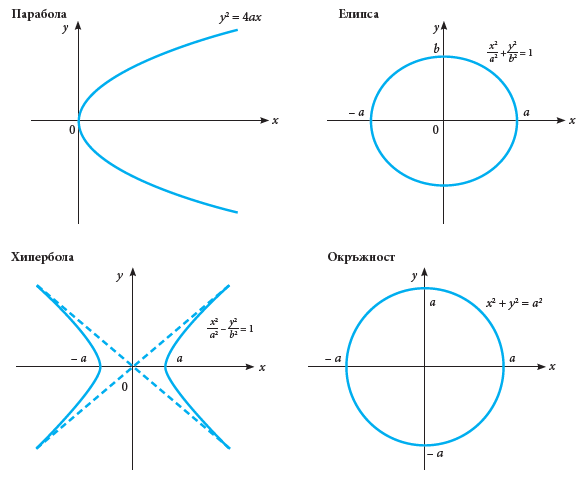
Фиг. 2: Коничните сечения (Източник: http://amsi.org.au/ESA_Senior_Years/SeniorTopic2/2a/2a_3links.html)
Елипса – затворена крива с два фокуса. Елипсата изглежда като сплеснат кръг, като сплеснатостта се определя от ексцентрицитета (бележи се с е и заема стойности от нула до по-малко от 1). Елипсата има 2 оси (голяма и малка), които минават през центъра и я разделят на 2 равни половини. Половините от осите се наричат голяма полуос (бележи се с а) и малка полуос (бележи се с b). Фокусите на елипсата лежат на големите полуоси. Разстоянието на фокусите от центъра се определя от произведението на а и е.
Окръжност – частен случай на елипса. Получава се при пресичане на прав кръгов конус с равнина, перпендикулярна на оста му. Ексцентрицитетът е точно e = 0.
Парабола – отворена крива с един фокус. Получава се при пресичане на конуса с равнина, успоредна на образувателната му. Ексцентрицитетът е e = 1.
Хипербола – отворена крива с два фокуса, състояща се от два клона. Тя е сечение на двата ръкава на конуса с равнина, която не е успоредна на негова образувателна. Ексцентрицитетът е e > 1.
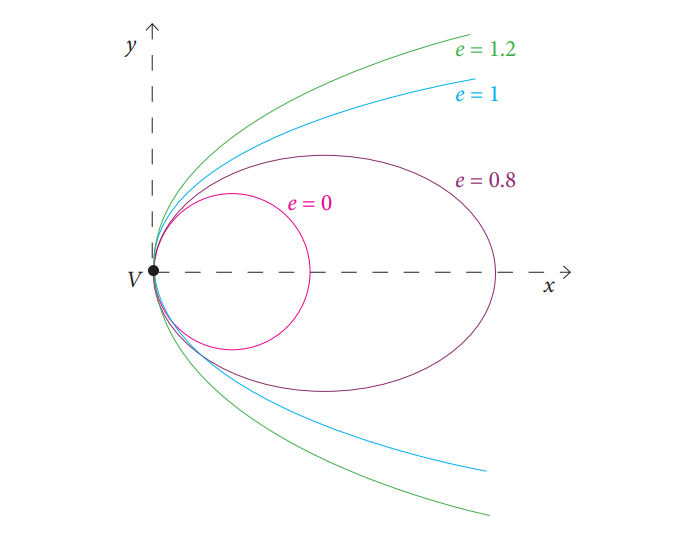
Фиг. 3: Ексцентрицитет на различните конични сечения (Източник: By Ag2gaeh – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index. php?curid=56338953)
Екцентрицитет
Характерен параметър, общ за всички сечения е ексцентрицитетът (e). Той може да се приеме като мярка за това колко голямо е отклонението на дадено конично сечение от кръг. Тогава за окръжност, ексцентрицитетът е нула (т.е. няма отклонение); за елипсата той ще е по-голям от нула, но по-малък от 1 (точната формула е e = ((a2 – b2)1/2) / a); за параболата ще е точно равен на 1; за хиперболата ще е по-голям от 1 (Фиг. 3)
Уравненията за кничните сечения са:
Ексцентрицитетът е: