- Задача 1: Движение около Слънцето
- Задача 2.: Луната е на разстояние... , но какво?!
- Задача 3: Това обича и съседът
- Задача 4: Извънземно и човек
- Задача 5: Газовият гигант наречен Юпитер
- Задача 6: Марс.....къде е?
- Задача 7: Полет до Марс по полуелипса
- Задача 8: Геостационарен спътник
- Задача 9: Сблъсък със Слънцето
- Задача 10: ЛЕК КАТО... СУПЕР ЧЕРНА ДУПКА!
Задача 6: Марс.....къде е?
Голямата полуос на орбитата на Марс е а голямата полуос на орбитата на Земята е
. Да предположим, че планетите обикалят в една и съща равнина в една и съща посока.
a) Определете периода на орбитата на Марс около Слънцето.
б) Определете ъгловата скорост на Марс около Слънцето, както и ъгловата скорост на Земята.
в) Тъй като планетите се движат в една и съща посока, извадете ъгловите скорости една от друга, за да получите отношението на ъгловите скорости една спрямо друга (вижте фигури 7 и 8).
г) Определете т. нар. синодичен орбитален период P, който е периодът, за който Земята, Марс и Слънцето отново се подреждат в една линия.
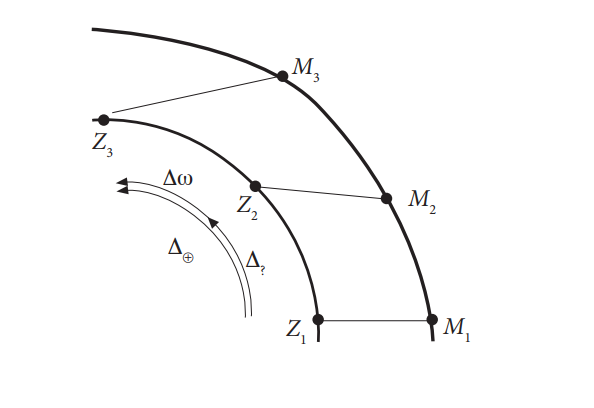
Фигура 7: Ъгловата скорост на Марс около Слънцето е по-малка от тази на Земята
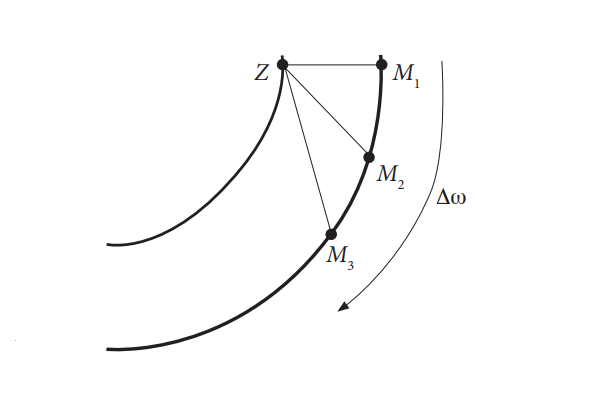
Фигура 8: От гледна точка на земния жител Марс се движи с ъглова скорост Δω
Решение:
a) Ще използваме Третия закон на Кеплер по същия начин, както в задачи 4 и 5: , следователно орбиталният период е T = 1,87 yr.
б) Ъгловата скорост се определя като „ъгълът, описан от радиус-вектора за единица време“. Тъй като в един орбитален период T радиус-векторът ще опише ъгъл 360°, средната ъглова скорост ще е равна на . Тъй като считаме, че орбитите на Земята и Марс са точно кръгови, това е и моментна ъглова скорост, която е една и съща във всеки момент.
Ъгловата скорост на Земята около Слънцето е
а на Марс ъгловата скорост около Слънцето е
в) Планетите се движат в една и съща посока, следователно относителната ъглова скорост е равна на
г) За синодичния период P се прилага: , следователно
Ако е необходимо, може да се получи и обобщителен резултат