Закони на Кеплер
Първи закон на Кеплер
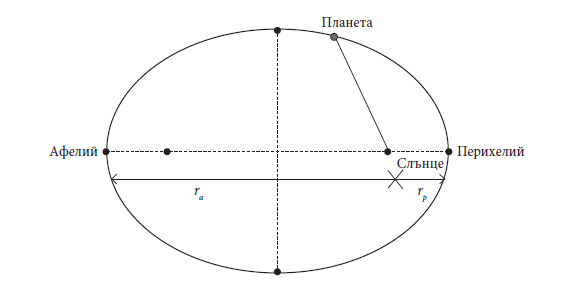
От Първия закон на Кеплер следва, че планетите се движат по равнинни затворени криви. Фиг. 2 показва орбитата на една планета със Слънцето в единия фокус. Точката на елипсата, която е най-близката до Слънцето, се нарича перихелий, а най-отдалечената точка се нарича афелий. Разстоянията от фокуса до перихелия и афелия са обозначенис rp и ra съответно. Фиг. 2 показва и разстоянието r от Слънцето до планетата. Фигура 2 може да се прочете по следния начин:
Втори закон на Кеплер
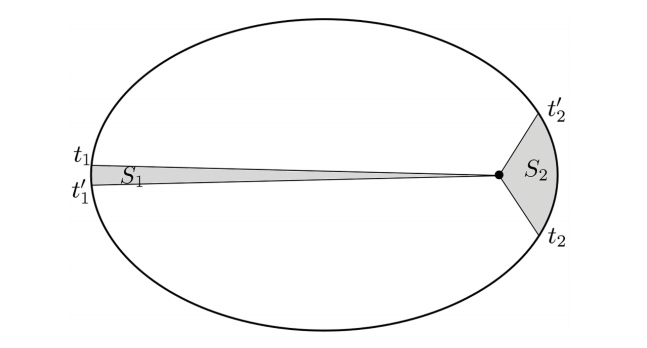
Смисълът на втория закон на Кеплер е илюстриран на Фиг. 3. Отбелязани са два времеви интервала 
, които отговарят на площите 
a 
. съответно, описани от радиус-вектора на планетата. От Втория закон на Кеплер следва, че ако 
, то 
.
Трети закон на Кеплер
Ако означим орбиталните периоди на две планети, обикалящи около Слънцето с T1 и T2, а дължините на големите полуоси на техните орбити с a1, a2, то
което четем като:
В Слънчевата система има смисъл орбиталните периоди да се изчисляват в земни години, а големите полуоси - в астрономически единици (съкращение „au“ от анл. „astronomical unit“). За Земята важи следното: 
au, 
= 1 год.
Забележка: Внимателният читател може да забележи, че тази формулировка на закона важи независимо от използваните единици. С други думи, можем да изчисляваме периода в години, както и в секунди или в часове – отношението важи. Същото важи и за голямата полуос. Тя може да бъде изчислявана в астрономически единици, но също така и в метри, километри и т.н.
Нека вземем този пример:
Отношението на периодите не зависи от мерните единици, в които изчисляваме, защото коефициентът на преобразуване е еднакъв (числителят и знаменателят се делят/умножават на едно и също число).
Сега ще продължим и ще покажем, че можем да работим дори с безразмерни величини. Нека дефинираме (безразмерните) относително разстояние aʹ и относителен период Tʹ, които показват колко разстоянието и периодът са по-големи от a и T:
където 
e голямата полуос,а 
е периодът на Земята.
Ако тогава a = 1,5 au, то aʹ = 1,5.