- Задача 1: Движение около Слънцето
- Задача 2.: Луната е на разстояние... , но какво?!
- Задача 3: Това обича и съседът
- Задача 4: Извънземно и човек
- Задача 5: Газовият гигант наречен Юпитер
- Задача 6: Марс.....къде е?
- Задача 7: Полет до Марс по полуелипса
- Задача 8: Геостационарен спътник
- Задача 9: Сблъсък със Слънцето
- Задача 10: ЛЕК КАТО... СУПЕР ЧЕРНА ДУПКА!
Задача 9: Сблъсък със Слънцето
Да предположим, че имаме контейнер, пълнен с опасен материал, от който трябва да се отървем и искаме да използваме Слънцето като един вид „място за изгаряне“. Трябва да изстреляме контейнера от Земята с такава скорост, че той да спре в свободно пространство и след това да започне да пада по права към Слънцето (вж. Фиг. 9). Използвайте подходящия за случая Трети закон на Кеплер и изчислете времето на падане на контейнера върху Слънцето.
Съвет: Контейнерът по време на своето падане чак до момента на сблъскване със Слънцето, ще премине отсечка, която може да разглеждаме като специален случай на елипса (елипса с a = e, b = 0).
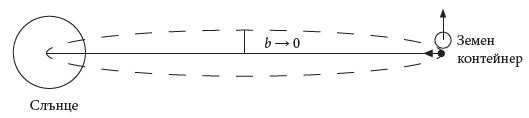
Фиг. 12: Контейнерът се движи по отсечка, която можем да си представим като елипса с много мъничка малка полуос. Началото на отсечката (вдясно) отговаря на точката на изстрелване, а краят на отсечката (вляво) отговаря на центъра на Слънцето. Фигурата не е пропорционална на действителните разстояния, тя е само илюстративна.
Решение:
От начертаната фигура разбираме, че голямата полуос на „елипсата“ е 
.
Ако използваме Третия закон на Кеплер във формата
, то
, и следователно 
.
Периодът е приблизително Т = 0,35 години = 128 дни. Контейнерът, обаче, няма да се върне в точката, от която е започнал да пада. Той ще изгори в Слънцето, преминавайки само половината от „елипсата“, така че времето на падане отговаря на половината от изчисления период, или 64 дни.
Забележка: От фигурата може да изглежда, че контейнерът ще стигне до Слънцето по-рано, отколкото за време
което, разбира се, е вярно. Важно е да се отбележи, че въпреки че размерите на Слънцето са „огромни“ (в сравнение с това, с което се срещаме в ежедневието си; само за да добиете представа посочваме, че радиусът на Слънцето е 
), те са нищожни в сравнение с разстоянието между Земята и Слънцето. В това приближение Слънцето може да се счита за точка с маса и затова предишното изчисление е направено добре.