- Задача 1: Движение около Слънцето
- Задача 2.: Луната е на разстояние... , но какво?!
- Задача 3: Това обича и съседът
- Задача 4: Извънземно и човек
- Задача 5: Газовият гигант наречен Юпитер
- Задача 6: Марс.....къде е?
- Задача 7: Полет до Марс по полуелипса
- Задача 8: Геостационарен спътник
- Задача 9: Сблъсък със Слънцето
- Задача 10: ЛЕК КАТО... СУПЕР ЧЕРНА ДУПКА!
Задача 5: Газовият гигант наречен Юпитер
Когато Юпитер е най-близко и най-далеч, разстоянията са и
, съответно. Нека приемем, че Земята се движи по кръгова орбита, а орбитите на Земята и Юпитер лежат в една равнина, вж. Фиг. 3.
След това определете:
a) перихелия и афелия на орбитата на Юпитер,
б) голямата и малката полуоси, линейния ексцентрицитет и числения ексцентрицитет,
в) периода на орбитата,
г) колко пъти скоростта на Юпитер е по-голяма в перихелия в сравнение с афелия.
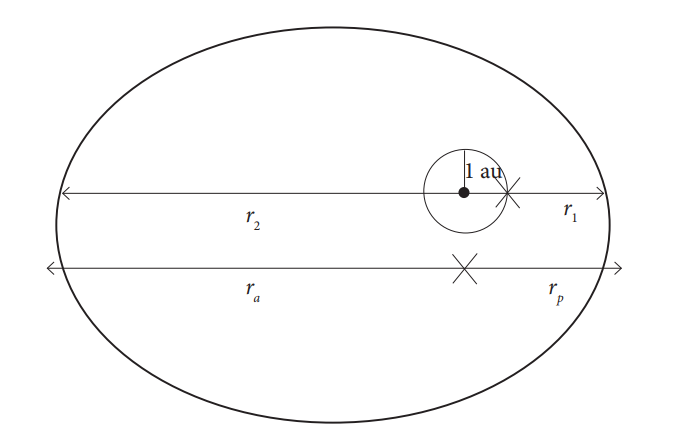
Фиг. 6: Към разбора на задачата
Решение:
a) Най-близкото разстояние от Юпитер до Слънцето е .
Най-голямото разстояние тогава е равно на .
б) За всяка една елипса определяме голямата полуос като , линейния ексцентрицитет както е показано на фигурата
, числения ексцентриситет е по дефиниция
, а малката полуос определяме от Питагоровата теорема
Виждаме, че орбитата на Юпитер е почти кръгова.
в) Ще работим като в в Задача 4. Ако искаме да използваме формулировката на Третия закон на Кеплер във вида , то тогава
,
Следователно, периодът е . години.
г) От Втория закон на Кеплер следва, че .