- Задача 1: Движение около Слънцето
- Задача 2.: Луната е на разстояние... , но какво?!
- Задача 3: Това обича и съседът
- Задача 4: Извънземно и човек
- Задача 5: Газовият гигант наречен Юпитер
- Задача 6: Марс.....къде е?
- Задача 7: Полет до Марс по полуелипса
- Задача 8: Геостационарен спътник
- Задача 9: Сблъсък със Слънцето
- Задача 10: ЛЕК КАТО... СУПЕР ЧЕРНА ДУПКА!
Задача 4: Извънземно и човек
Комета обикаля около Слънцето. Нейният перихелий е на разстояние а афелият е на разстояние
вж. Фиг. 2.
Определете:
a) голямата и малката полуоси, линейния ексцентрицитет и числения ексцентрицитет,
б) периода на кометата,
в) колко пъти скоростта на кометата е по-голяма в перихелия в сравнение с афелия.
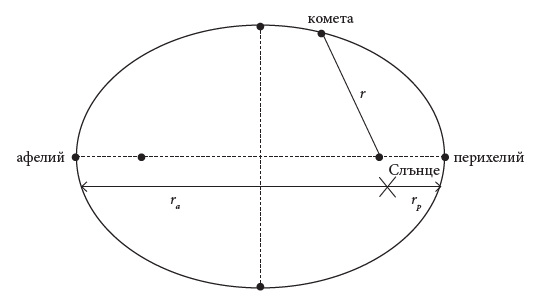
Фиг. 5: Схематична скица на траекторията на кометата
Решение:
От геометрията на елипсата получаваме: ,
,
.
.Орбитата на кометата (предсказуемо) е много ексцентрична.
б) Третият закон на Кеплер ще запишем като където aʹ е в астрономически единици, Tʹ е в години, а М’ е в слънчеви маси. Тъй като ние се занимаваме с движението на комета в Слънчевата система, то автоматично се изпълнява
Mʹ = 1. Следователно . Както знаем, при дадената формулировка на закона всички величини са безразмерни. Числовата стойност показва колко пъти периодът е по-голям от периода на въртене на Земята около Слънцето (т.е. колко пъти периодът е по-голям от една година). Следователно, периодът е
.
Възможно е да се използва и друго (но разбира се еквивалентно) изписване на Третия закон на Кеплер. Ако работим в SI системата, ще запишем Третия закон на Кеплер така: .
Знаем масата на Слънцето, която е, гравитационната константа е
а голямата полуос е
.
От Третия закон на Кеплер изразяваме периода:
в) От Втория закон на Кеплер следва .