Úvod
Kužeľosečky sú jednou z najstarších a najdlhšie študovaných geometrických kriviek. Verí sa, že ich pôvodne objavil Menehm (jeden z učiteľov Alexandra Veľkého) v 4. st. p. n. l. Neskôr ich študoval Eukleides z Alexandrie (asi 300 p. n. l.) a Apollónios z Pergy (asi 200 p. n. l.), pričom Apollónius bol ten, kto im dal názvy, ktoré používame aj dnes – elipsa, parabola a hyperbola. V matematike je kužeľosečka definovaná ako krivka, ktorú je možné získať prierezom kužeľovej plochy s rovinou (Obr. 1). Kužeľosečky majú dôležité uplatnenie v astronómii: používajú sa na opis pohybu nebeských telies pod vplyvom gravitácie. Dráhy týchto pohybov sa nazývajú obežné dráhy (alebo orbity) nebeských telies.
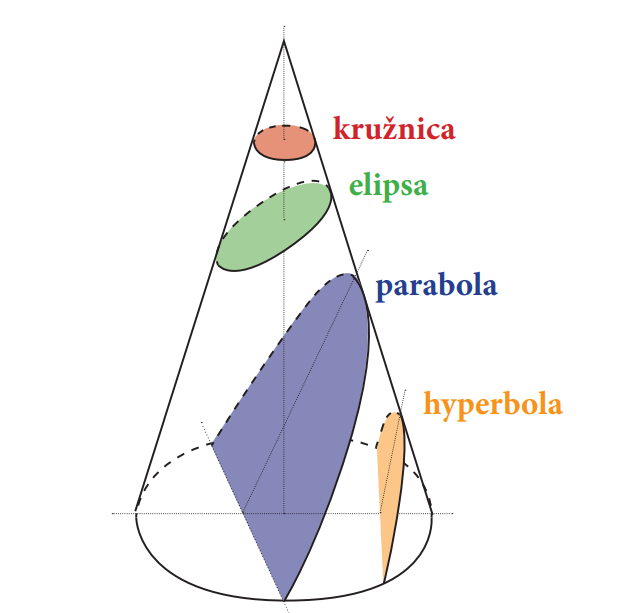
Obrázok 14: Kužeľosečky
(zdroj: http://commons.wikimedia.org/wiki/User:Magister_Mathematicae - File:Secciones_cónicas.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=18556148)
Typy kužeľosečiek. Parametre
Typy kužeľosečiek
V matematike je kužeľosečka definovaná ako krivka, ktorú je možné získať prierezom kužeľovej plochy s rovinou.
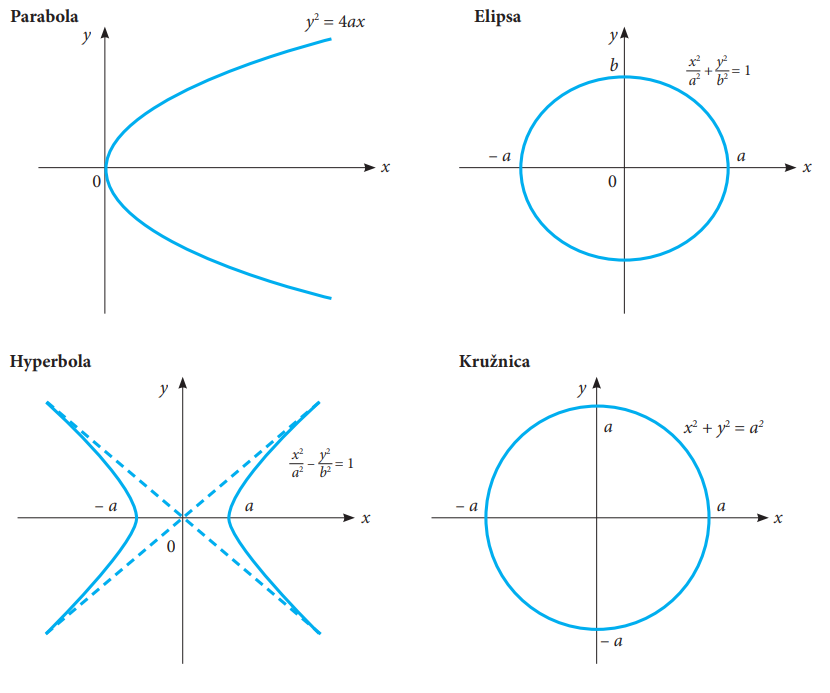
Obrázok 15: Kužeľosečky
(zdroj: http://amsi.org.au/ESA_Senior_Years/SeniorTopic2/2a/2a_3links.html)
Elipsa – uzavretá krivka s dvoma ohniskami. Elipsa má tvar splošteného kruhu, pričom sploštenosť je daná excentricitou (zaznačuje sa a má hodnoty od 0 do menej ako 1). Elipsa má dve osi (veľká a malá os), ktoré prechádzajú stredom a delia ju na dve rovnaké polovice. Polovičky osí sa nazývajú veľká polos (označuje sa písmenom „a“) a malá polos (označuje sa písmenom „b“). Ohniská elipsy ležia na veľkých polosiach. Vzdialenosť ohnísk od stredu je určená súčinom a a e (pozri obrázok).
Kružnica – špeciálny prípad elipsy. Získava sa priesečníkom priameho kruhového kužeľa s rovinou kolmou na jeho os. Excentricita je presne = 0.
Parabola – otvorená krivka s jedným ohniskom. Získava sa priesečníkom kužeľa s rovinou rovnobežnou s jeho tvorbou. Excentricita je e = 1.
Hyperbola – otvorená krivka, ktorá pozostáva z dvoch vetiev, má dve ohniská a dve asymptoty. Je to priečny rez dvoma rukávmi kužeľa s rovinou, ktorá nie je rovnobežná s jeho vytvorením. Excentricita je > 1.
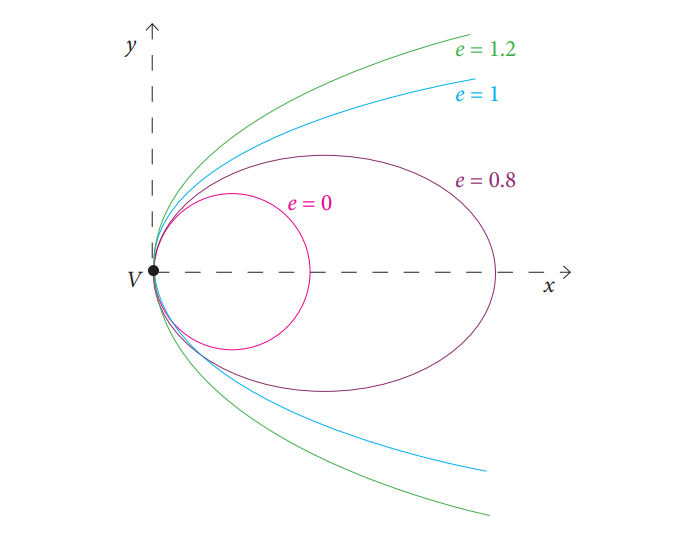
Obrázok 16: Excentricita rôznych kužeľosečiek
(zdroj: By Ag2gaeh – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=56338953)
Exentricita
Charakteristickým parametrom spoločným pre všetky sekcie je excentricita (e). Môže sa to prijať ako mierka toho, aká veľká je odchýlka kužeľosečky od kruhu. Potom pre kružnicu je excentricita nula (t. j. žiadna odchýlka); v prípade elipsy bude väčšia ako 0, ale menšia ako 1 (presný vzorec); pre parabolu to bude presne 1; pre hyperbolu to bude väčšie ako 1 (Obr. 16).
Rovnice kužeľosečiek:
Excentricita je: