- Úkol 1 Radiány, nebo stupně?
- Úkol 2 Mars v opozici a kvadratuře
- Úkol 3 Měříme Merkur a Venuši
- Úkol 4 „Merkuan“
- Úkol 5 Země z Marsu
- Úkol 6 Jak velký je Měsíc?
- Úkol 7 Měsíc po druhé
- Úkol 8 Parametry trajektorie planet
- Úkol 9 Jako z jiné planety
- Úkol 10 Nohama pevně na Zemi
- Úkol 11 Řeku, jak velká je Země?
- Úkol 12 Měsíc v akci po třetí
Úkol 6: Jak velký je Měsíc?
a) Střední vzdálenost Země-Slunce je d = 1 au = 1,496 ⋅ 108 km, poloměr Slunce je R☉ = 6,955 ⋅ 105 km. Určete úhlovou velikost Slunce pro pozorovatele na Zemi.
b) Ze znalosti hmotnosti Země M⊕ = 5,97 ⋅ 1024 kg a doby oběhu Měsíce kolem Země T = 27,3 dní z třetího Keplerova zákona vzdálenost Měsíce od Země. Hmotnost Měsíce pro odhad vzdálenosti neuvažujte.
c) Protože víte, dochází k částečným i úplným zatměním Slunce, odhadněte skutečné rozměry Měsíce. Ilustrace jevu je na obr. 2.

(Zdroj: https://apod.nasa.gov/
apod/ap160831.html, cit. 5.8.2018)

(Zdroj: https://www.nasa.gov/multimedia/
imagegallery/image_feature_1249.html, cit. 5.8.2018)
d) Jaká by byla úhlová velikost Země pro astronauta na Měsíci, když by se Měsíc pohyboval po přesně kruhové dráze? Jak velkou část povrchu Země astronaut vidí (viz obr. 3 a 4)? Výsledek vyjádřete v procentech. Poloměr Země je R⊕ = 6 378 km.
Nápověda: Část povrchu Země, kterou pozorovatel vidí, odpovídá povrchu kulového vrchlíku. Plocha kulového vrchlíku (bez podstavy) je , kde R je polomeř sféry a v je výška kulové úseče, viz obrázek obr. 4.
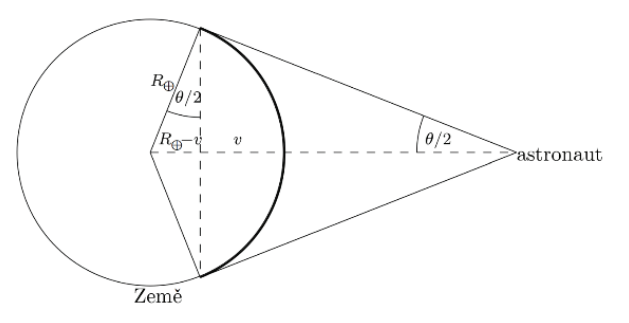
Obr. 4: Ilustrace astronautova pohledu na Zem
Řešení
a) Vyjdeme z přibližného vztahu pro úhlovou velikost:.
Mohli bychom též vyjít z přesného vztahu
resp.
.
Mohli by sme vyjsť aj z presného vzťahu tg tg . Výsledky jsou samozřejmé stejné, viz. Úloha I.
b) Vyjdeme z 3. Keplerova zákona .
c) Protože dochází k částečným a úplným zatmění Slunce, je úhlová velikost Měsíce srovnatelná s úhlovou velikostí Slunce, tedy .Poloměr Měsíce určíme ze vztahu: R =
. Skutečný poloměr Měsíce je 1 737 km, tedy náš výsledek souhlasí dobře se skutečností.
d) Vyjdeme z přibližného vztahu pro úhlovou velikost: .Z obr. 2 zjevně platí:
.
Buď můžeme výšku kulového vrhlíku spočítat přímo ze zadaných hodnot, nebo z vypočítané hodnoty úhlové velikosti Země. Dosadíme do pomocného vzorce pro plochu kulového vrchlíku . Vzorec pro plochu koule je
, proto
pro poměr plochy kulového vrchlíku k celé kouli je: . Astronaut vidí téměř celou jednu stranu Země.
Z poslední rovnice je jasné, že čím bude astronaut dále od Země (vzdálenost přitom
udává hlavní poloosa, protože odpovídá poloměru kruhové orbity), tím bude člen blíže nulo a astronaut uvidí větší část Země, maximálně však 50%. Bude-li
naopak astronaut těsně nad povrchem Země, bude člen blízko 1 a poměr
bude téměř nulový.