Úvod

V tomto příspěvku představíme tzv. aspekty, význačné polohy planet ve Sluneční soustavě z pohledu Země. Postupně vysvětlíme pojmy: konjunkce, opozice, elongace, kvadratura a podíváme se, jak lze určit vzdálenost planety, umístěnou v některém z těchto význačných bodů, od Země.

Dále v příspěvku vysvětlíme, jak je definovaná úhlová velikost tělesa a jak nám její znalost, společně se znalostí vzdáleností tělesa, pomůže určit skutečné rozměry tělesa. K tomu jsme obecně nuceni pracovat s goniometrickými funkcemi. Vysvětlíme si však, proč v případech, kdy se tělesa nachází od pozorovatele ve velké vzdálenosti, můžeme od goniometrických funkcí odhlédnout a výpočet si zjednodušit. Zatímto účelem přirozeně zavedeme velmi užitečné úhlové jednotky, tzv. radiány.

Vzdálenosti a velikosti

Typické vzdálenosti ve Sluneční soustavě

Střední vzdálenost Země–Slunce je km poloměr Země je polomer Země je km. V tab. 1 jsou zaznamenány střední vzdálenosti planet od Slunce a jejich poloměry v násobcích poloměrů Země. Pro srovnání uvádíme i poloměr Slunce. Rozměry Slunce se zdají být obrovské ve srovnání s ostatními planetami, je ale zajímavé přepočítat poloměr Slunce do astronomických jednotek . Z toho je vidět, že planety ani Slunce mnoho prostoru Sluneční soustavy nezaujímají.

Tab. 1: Střední vzdálenosti planet ve Sluneční soustavě a poloměry planet a Slunce

Těleso	Vzdálenost od Slunce [au]	R/R_⊕
Slunce	0	109
Merkur	0,39	0,38
Venuše	0,72	0,95
Země	1,00	1,00
Mars	1,52	0,53
Jupiter	5,20	11,2
Saturn	9,54	9,45
Uran	19,2	4,01
Neptun	30,07	3,88

Aspekty planet

Z pohledu Země rozlišujeme několik význačných poloh planet, tzv. aspektů, které jsou schematicky zakresleny v obr. 1 a jejich popis je uveden níže.

1. Konjunkce

U vnitřních planet (Merkur, Venuše) rozeznáváme horní a dolní konjunkci. Horní konjunkce je okamžik, kdy se planeta nachází na opačné straně od Slunce (Slunce je mezi Zemí a vnitřní planetou). Dolní konjunkce nastává, je-li planeta mezi Zemí a Sluncem. Vnější planeta (Mars, Jupiter, Saturn, Uran, Neptun)se může nacházet pouze vhorní konjunkci.

Je-li planeta v konjunkci, vychází a zapadá společné se Sluncem, nachází se na denní obloze a není pro nás pozorovatelná.

2. Opozice

Okamžik, kdy je vnější planeta Zemi nejblíže, resp. Země je mezi planetou a Sluncem, se nazývá opozice. V době opozice jsou nejpříznivější podmínky pro pozorování planety, neboť planeta vychází při západu slunce a zapadá při východu Slunce (je tak pozorovatelná po celou noc) a planeta se jeví v dalekohledu největší (tj. má největší úhlovou velikost)

3. Elongace

Elongace je úhlová vzdálenost mezi vnitřní planetou a Sluncem. Při západní elongaci planeta vychází i zapadá dříve než slunce. Při východní elongaci vychází i zapadá slunce dříve než planeta. Největší úhlová vzdálenost planety od Slunce se nazývá maximální elongace2. Maximální elongace Merkuru je23°, Venuše 47°.

4. Kvadratúra

Kvadratura je okamžik, kdy úhel Slunce-Země-vnější planeta je pravý. V kvadratuře se mohou nacházet pouze vnější planety.

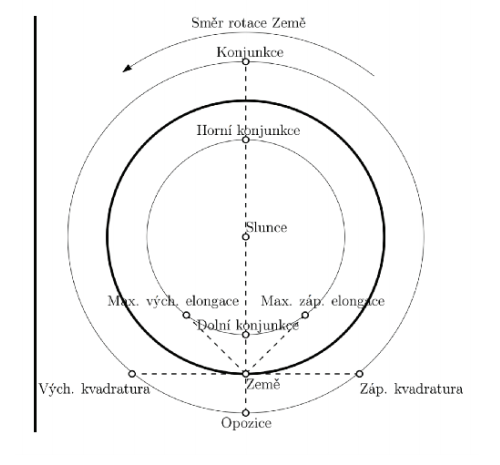
Obr. 1: Schéma možních konfigurácí planet

Úhlová velikosti objektů

Je přirozené, že pokud se objektyod nás nachází ve velké vzdálenosti, zdají se nám být menší, než kdyby se nacházely v naší těsné blízkosti. Přesto se jejich fyzické rozměry nemění. Abychom byli schopni tuto skutečnost kvalitativně popsat, zavádíme veličinu úhlové velikosti θ, jejíž význam vystihuje obr. 2. Obrázek nám poskytuje jasnou představu, jak se má úhlová velikost počítat:

Úhel θ pak dostaneme jako: . Jen pro představu, pro Slunce o poloměru , ve vzdálenosti vychází úhlová velikosti θ☉ ≐ 32'. Nedá se asi divit, že úhlové velikosti planet ve Sluneční soustavě pak vychází v řádu jednotek až desítek úhlových vteřin.

Ďalej si ukážeme, ako zjednodušiť vzťah pre výpočet uhlovej veľkosti, ak je malá. Na to bude potrebné zaviesť „nové“ jednotky rovinného uhla, tzv. radiány.

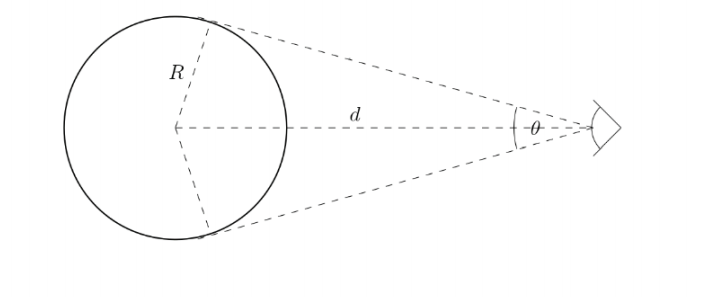
Obr. 2: K definice úhlové velikosti

Radiány

Radiány jsou nejpřirozeněji definované jednotky rovinného úhlu. Představme si soustředné kružnice jako na obr. 3. Úhel θ je definován jako podíl délky odpovídajícího oblouku a poloměru kružnice. Z obr. 3 je vidět, že úhel nezávisí na konkrétní délce oblouku nebo poloměru:

, ipouze na jejich poměru, což je přirozené a správné.Už víme, jak lze definovat úhel, pořád ale ještě nevíme, co „radián“.

Z toho, jak jsme definovali úhel (délka oblouku dělená poloměrem) by se zdálo, že úhel nemá rozměr, resp. jednotkou úhlu je „jednička“. A přesně tomu se říká radián! Také bychom pro rozměr úhlu mohli psát: . Bezrozměrných veličin existuje nemalé množství. Tím, že budeme k číslům psát „rad“ upozorňujeme na to, že číslo odpovídá velikosti úhlu. Protože poloměr kružnice je , je plný úhel je plný úhel . Samozřejmě, . Předposlední rovnost dává převodní vztah mezi radiány a stupni: .

Dále si uvědomme, že čím bude úhel θ menší, tím více bude oblouk (od délce Δs) podobný úsečce. Toho využijeme v dalším odstavci.

Obr. 3: K zavedení radiánů

Úhlová velikost po druhé

Nyní si představme, že by rozměr kulového objektu byl výrazně menší nežjeho vzdálenost od nás. Jak jsme naznačili výše, pro velké vzdálenosti lze (dostatečně malou) délku oblouku dobře odhadnout úsečkou a naopak. V takovém případě lze pro úhlovou velikost objektu (v radiánech) psát:

Samozřejmě, vztah musí dávat pro malé úhlové velikosti, pro které je odvozený, stejné výsledky jako pro dříve odvozený vztah, tedy , přičemž úhel θ počítá v radiánech (kalkulačka dokáže spočítat tangens jak ve stupních, tak v radiánech).

Zdroje a doporučená literatura

[1] Mikulčák J., Macháček M., Zemánek F.: Matematické,fyzikální a chemické tabulky a vzorce pro SŠ, Prometheus, Praha, 2003

[2] Široký J., Široká M.: Základy astronomie v příkladech, SPN, Praha, 1966, online odkaz: http://physics.ujep.cz/~zmoravec/astronomie/siroky/siroky.html, cit. 8.7.2018