Úvod
V tomto texte predstavíme tzv. aspekty, význačné polohy planét v Slnečnej sústave z pohľadu Zeme. Postupne vysvetlíme pojmy: konjunkcia, opozícia, elongácia, kvadratúra a pozrieme sa, ako možno určiť vzdialenosť planéty, umiestnenej v niektorom z týchto význačných bodov od Zeme.
Ďalej vysvetlíme, ako je definovaná uhlová veľkosť telesa a ako nám jej znalosť, spoločne so znalosťou vzdialenosti telesa, pomôže určiť skutočné rozmery telesa. Na to sme všeobecne nútení pracovať s goniometrickými funkciami. Vysvetlíme si však, prečo v prípadoch, keď sa telesá nachádzajú od pozorovateľa vo veľkej vzdialenosti, môžeme od goniometrických funkcií odhliadnuť a výpočet si zjednodušiť. Za týmto účelom prirodzene zavedieme veľmi užitočné uhlové jednotky, tzv. radiány.
Vzdialenosti a veľkosti
Typické vzdialenosti v Slnečnej sústave
Stredná vzdialenosť Zem – Slnko je km polomer Zeme je
polomer Zeme je
km. V Tab. 1 sú zaznamenané stredné vzdialenosti planét od Slnka a ich polomery v násobkoch polomerov Zeme. Pre porovnanie uvádzame aj polomer Slnka. Rozmery Slnka sa zdajú byť obrovské v porovnaní s ostatnými planétami, je ale zaujímavé prepočítať polomer Slnka do astronomických jednotiek:
km, polomer Zeme je
km. V Tab. 1 sú zaznamenané stredné vzdialenosti planét od Slnka a ich polomery v násobkoch polomerov Zeme. Pre porovnanie uvádzame aj polomer Slnka. Rozmery Slnka sa zdajú byť obrovské v porovnaní s ostatnými planétami, je ale zaujímavé prepočítať polomer Slnka do astronomických jednotiek:
. Z toho je vidieť, že planéty ani Slnko mnoho priestoru Slnečnej sústavy nezaberajú.
Tab. 1: Stredné vzdialenosti planét v Slnečnej sústave a polomery planét a Slnka
| Teleso | Vzdialenosť od Slnka [au] | R/R⊕ |
| Slnko | 0 | 109 |
| Merkúr | 0,39 | 0,38 |
| Venuša | 0,72 | 0,95 |
| Zem | 1,00 | 1,00 |
| Mars | 1,52 | 0,53 |
| Jupiter | 5,20 | 11,2 |
| Saturn | 9,54 | 9,45 |
| Urán | 19,2 | 4,01 |
| Neptún | 30,07 | 3,88 |
Aspekty planét
Z pohľadu Zeme rozlišujeme niekoľko význačných polôh planét, tzv. aspektov, ktoré sú schematicky zakreslené na Obr.1 a ich popis je uvedený nižšie.
1. Konjunkcia
Pri vnútorných planétach (Merkúr, Venuša) rozoznávame hornú a dolnú konjunkciu. Horná konjunkcia je okamih, kedy sa planéta nachádza na opačnej strane od Slnka (Slnko je medzi Zemou a vnútornou planétou). Dolná konjunkcia nastáva, ak je planéta medzi Zemou a Slnkom. Vonkajšia planéta (Mars, Jupiter, Saturn, Urán, Neptún) sa môže nachádzať iba v hornej konjunkcii.
Ak je planéta v konjunkcii, vychádza a zapadá spoločne so Slnkom, nachádza sa na dennej oblohe a nie je pre nás pozorovateľná.
2. Opozícia
Okamih, kedy je vonkajšia planéta k Zemi najbližšie, resp. Zem je medzi planétou a Slnkom, sa nazýva opozícia. V čase opozície sú najpriaznivejšie podmienky pre pozorovanie planéty, pretože planéta vychádza pri západe slnka a zapadá pri východe Slnka (je tak pozorovateľná po celú noc) a planéta sa javí v ďalekohľade najväčšia (t. j. má najväčšiu uhlovú veľkosť)
3. Elongácia
Elongácia je uhlová vzdialenosť medzi vnútornou planétou a Slnkom. Pri západnej elongácii planéta vychádza aj zapadá skôr ako Slnko. Pri východnej elongácii vychádza aj zapadá Slnko skôr ako planéta. Najväčšia uhlová vzdialenosť planéty od Slnka sa nazýva maximálna elongácia2 . Maximálna elongácia Merkúru je 23°, Venuše 47°.
4. Kvadratúra
Kvadratúra je okamih, kedy uhol Slnko – Zem – vonkajšia planéta je pravý. V kvadratúre sa môžu nachádzať iba vonkajšie planéty
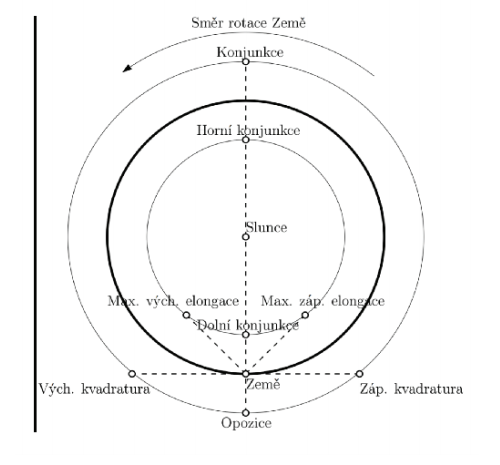
Obrázok 1: Schéma možných konfigurácií planét
Uhlové veľkosti objektov
Je prirodzené, že ak sa objekty od nás nachádzajú vo veľkej vzdialenosti, zdajú sa nám byť menšie, než keby sa nachádzali v našej tesnej blízkosti. Napriek tomu sa ich fyzické rozmery nemenia. Aby sme boli schopní túto skutočnosť kvalitatívne popísať, zavádzame veličinu uhlovej veľkosti θ, ktorej význam vystihuje Obr. 2. Obrázok nám poskytuje jasnú predstavu, ako sa má uhlová veľkosť počítať:
Uhol θ potom dostaneme ako: Iba pre predstavu, pre Slnko s polomerom θ potom dostaneme ako:
. Len pre predstavu, pre Slnko s polomerom
, vo vzdialenosti θ potom dostaneme ako:
. Iba pre predstavu, pre Slnko s polomerom
, vo vzdialenosti
vychádza uhlová veľkosť θ potom dostaneme ako:
. Iba pre predstavu, pre Slnko s polomerom
vo vzdialenosti
vychádza uhlová veľkosť θ☉ ≐ 32'. Nemôžeme sa asi čudovať, že uhlové veľkosti planét v Slnečnej sústave potom vychádzajú v ráde jednotiek až desiatok uhlových sekúnd.
Ďalej si ukážeme, ako zjednodušiť vzťah pre výpočet uhlovej veľkosti, ak je malá. Na to bude potrebné zaviesť „nové“ jednotky rovinného uhla, tzv. radiány
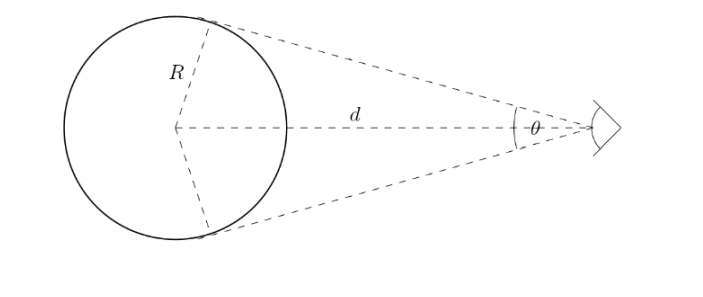
Obrázok 2: K definícii uhlovej veľkosti
Radiány
Radiány sú najprirodzenejšie definované jednotky rovinného uhla. Predstavme si sústredné kružnice ako na Obr. 3. Uhol θ je definovaný ako podiel dĺžky zodpovedajúceho oblúka a polomeru kružnice. Z Obr. 3 je vidieť, že uhol nezávisí od konkrétnej dĺžky oblúka alebo polomeru: θ je definovaný ako podiel dĺžky zodpovedajúceho oblúka a polomeru kružnice. Z Obr. 3 je vidieť, že uhol nezávisí od konkrétnej dĺžky oblúka alebo polomeru:
3 , iba od ich pomeru, čo je prirodzené a správne. Už vieme, ako možno definovať uhol, stále ale ešte nevieme, čo je to „radián“. Z toho, ako sme definovali uhol (dĺžka oblúka delená polomerom) by sa zdalo, že uhol nemá rozmer, resp. jednotkou uhla je „jednotka“. A presne tomu sa hovorí radián! Tiež by sme pre rozmer uhla mohli písať:
Bezrozmerných veličín existuje nemalé množstvo. Tým, že budeme k číslam písať „rad“ upozorňujeme na to, že číslo zodpovedá veľkosti uhla. Pretože polomer kružnice je
, je plný uhol
je plný úhel
. Samozrejme,
, je plný uhol
. Samozrejme,
. Predposledná rovnosť dáva prevodný vzťah medzi radiánmi a stupňami:
, je plný uhol
. Samozrejme,
. Predposledná rovnosť dáva prevodný vzťah medzi radiánmi a stupňami:
, je plný uhol
. Samozrejme,
. Predposledná rovnosť dáva prevodný vzťah medzi radiánmi a stupňami:
.
Ďalej si uvedomme, že čím bude uhol θ menší, tým viac bude oblúk (od dĺžky θ menší, tým viacej bude oblúk (od dĺžky Δs) podobný úsečke. To využijeme v ďalšom odseku.
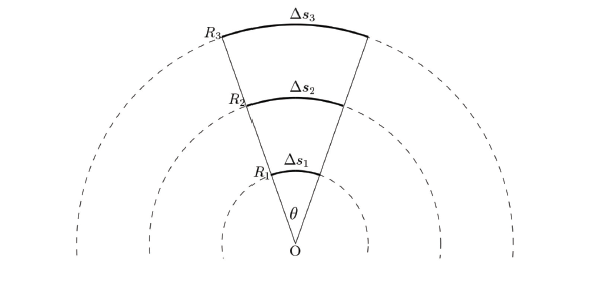
Obrázok 3: K zavedeniu radiánov
Uhlová veľkosť druhýkrát
Teraz si predstavme, že by rozmer guľového objektu bol výrazne menší ako jeho vzdialenosť od nás. Ako sme naznačili vyššie, pre veľké vzdialenosti možno (dostatočne malú) dĺžku oblúka dobre odhadnúť úsečkou a naopak. V takom prípade je možné pre uhlovú veľkosť objektu (v radiánoch) písať:
Samozrejme, vzťah musí dávať pre malé uhlové veľkosti, pre ktoré je odvodený, rovnaké výsledky ako pre predtým odvodený vzťah, teda , pričom uhol
, pričom uhol θ sa počíta v radiánoch (kalkulačka dokáže spočítať tangens v stupňoch aj v radiánoch).
Zdroje a odporúčaná literatúra
[1] Mikulčák J., Macháček M., Zemánek F.: Matematické,fyzikální a chemické tabulky a vzorce pro SŠ, Prometheus, Praha, 2003
[2] Široký J., Široká M.: Základy astronomie v příkladech, SPN, Praha, 1966, online odkaz: http://physics.ujep.cz/~zmoravec/astronomie/siroky/siroky.html, cit. 8.7.2018