- Úloha 1 Radiány, alebo stupne?
- Úloha 2 Mars v opozícii a kvadratúre
- Úloha 3 MERIAME MERKÚR A VENUŠU
- Úloha 4 „MERKUAN“
- Úloha 5 Zem z Marsu
- Úloha 6 Aký veľký je mesiac?
- Úloha 7 Mesiac druhýkrát
- Úloha 8 Parametre trajektórie planét
- Úloha 9 Ako z inej planéty...
- Úloha 10 Nohami pevne na Zemi...
- Úloha 11 Grék, aká veľká je zem?
- Úloha 12 MESIAC V AKCII PO TRETIE
Úloha 12: MESIAC V AKCII PO TRETIE
a) Na Obr. 6 je zachytené úplné zatmenie Mesiaca. S pomocou Obr. 6 a časov odhadnite, koľkokrát je polomer tieňa Zeme väčší ako polomer Mesiaca.
b) Ak je uhlová veľkosť Slnka θ☉ = 32', polomer Zeme je θ☉ = 32', polomer Zeme je R⊕ = 6 378 km a polomer kruhového orbitu θ☉ =32‘, polomer Zeme je R⊕ = 6 378 km a polomer kruhového orbitu a2 = 384 400 km, spočítajte s pomocou výsledku z bodu a) polomer Mesiaca. Obr. 7 vám môže pomôcť.
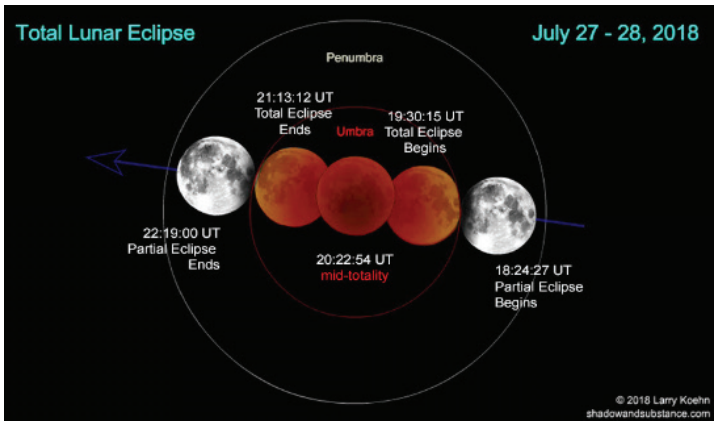
Obrázok 6: Zatmenie Mesiaca
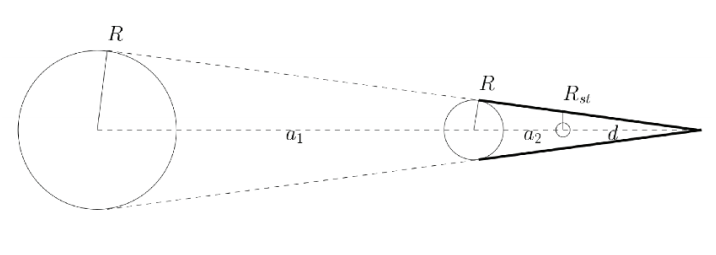
Obrázok 7: Zatmenie Mesiaca – rozbor situácie
Riešenie
a) Z časov uvedených na obrázku je zrejmé, že Mesiacu trvalo približne 1 hod 6 min vstúpiť do Zemského tieňa. V tomto tieni potom zotrval približne 2 hod 49 min. Pomer týchto časov potom zodpovedá pomeru priemeru tieňa Zeme a polomeru Mesiaca:
Pretože prechod Mesiaca cez Zemský tieň nie je presne centrálny, bude pomer v skutočnosti o trochu väčší.
b) Z náčrtku vyplýva nasledujúce: . Pretože
, je možné ľavú stranu prvej rovnosti písať ako
, je možné ľavú stranu prvej rovnosti písať ako
, čo sa rovná
, je možné ľavú stranu prvej rovnosti písať ako
, čo sa rovná
. Z prvej rovnosti tak už jednoducho vyjadríme
, je možné ľavú stranu prvej rovnosti písať ako
, čo sa rovná
. Z prvej rovnosti tak už ľahko vyjadríme
. Z druhej rovnosti dostávame
je možné ľavú stranu prvej rovnosti písať ako
, čo sa rovná
. Z prvej rovnosti tak už jednoducho vyjadríme
. Z druhej rovnosti dostávame
.
Polomer Mesiaca potom dostávame ako: , e možné ľavú stranu prvej rovnosti písať ako
, čo sa rovná
. Z prvej rovnosti tak už jednoducho vyjadríme
. Z druhej rovnosti dostávame
. Polomer Mesiaca potom dostávame ako:
. Skutočný polomer Mesiaca je 1 737 km, výsledok tak dáva rozumný odhad.