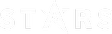Úloha 2: Trpasličie planéty a ich trajektórie
Úloha: Urči vzdialenosti trpasličích planét v príslní a odslní. Usporiadaj trpasličie planéty vzostupne podľa vzdialenosti od Slnka v príslní a odslní. Spočítaj pre každý objekt súčet vzdialeností v príslní a odslní. Porovnaj výslednú hodnotu s dvojnásobkom hlavnej polosi.
(Pomôcka: Vzdialenosť v príslní je a(1 – e), v odslní a(1 – e), v odsluní a(1 + e).)
Riešenie:
| Názov | Hlavná polos a (au) |
Výstrednosť trajektórie e (–) |
Vzdialenosť v príslní rP (au)< |
Vzdialenosť v odslní rP (au) |
rP + rA (au) |
2a (au) |
| Ceres | 2,77 | 0,0758 | 2,56 | 2,98 | 5,54 | 5,54 |
| Pluto | 39,5 | 0,2488 | 29,7 | 49,3 | 79 | 79 |
| Haumea | 43,2 | 0,191 | 34,9 | 51,5 | 86,4 | 86,5 |
| Makemake | 45,7 | 0,156 | 38,6 | 52,8 | 91,4 | 91,4 |
| Eris | 67,8 | 0,441 | 37,9 | 97,7 | 135,6 | 135,6 |
Väčšina objektov slnečnej sústavy sa pohybuje mimo rovinu ekliptiky, v ktorej obieha Zem okolo Slnka. Obežná rovina objektu zviera so základnou rovinou ekliptiky uhol, ktorý označujeme i, od slova inklinácia (sklon trajektórie). Skúsime započítať vplyv sklonu obežnej roviny objektu. Pre tento prípad budeme potrebovať goniometrické funkcie sínus a kosínus.
Úloha: Urči vzdialenosti trpasličích planét v príslní a odslní, ak ich premietneme do roviny ekliptiky a zahrnieme sklon ich obežných trajektórií. Ako ďaleko od roviny ekliptiky sa trpasličie planéty dostanú, ak sa nachádzajú v príslní alebo odslní.
Riešenie:
| Názov | Hlavná polos a (au) |
Výstrednosť trajektórie e (–) |
Sklon trajektórie i (°) |
Vzdialenosť v príslní v rovine ekliptiky (au) |
Vzdialenosť v odslní v rovine ekliptiky (au) |
Vzdialenosť od ekliptiky v príslní (au) |
Vzdialenosť od ekliptiky v odslní (au) |
| Ceres | 2,77 | 0,0758 | 11 | 2,51 | 2,93 | 0,49 | 0,57 |
| Pluto | 39,5 | 0,2488 | 17 | 28,4 | 47,1 | 8,7 | 14,4 |
| Haumea | 43,2 | 0,191 | 28 | 30,8 | 45,5 | 16,4 | 24,2 |
| Makemake | 45,7 | 0,156 | 29 | 33,8 | 46,2 | 18,7 | 25,6 |
| Eris | 67,8 | 0,441 | 44 | 27,3 | 70,3 | 26,3 | 67,9 |
Vzdialenosť v príslní v rovine ekliptiky (pre Ceres):
a (1 – e) cos i = 2,77 (1 – 0,0758) cos 11° au = 2,51 au
Vzdialenosť v odslní v rovine ekliptiky (pre Ceres):
a (1 + e) cos i = 2,77 (1 + 0,0758) cos 11° au = 2,93 au
Vzdialenosť od ekliptiky v príslní (pre Ceres):
a (1 – e) sin i = 2,77 (1 – 0,0758) sin 11° au = 0,49 au
Vzdialenosť od ekliptiky v odslní (pre Ceres):
a (1 + e) sin i = 2,77 (1 + 0,0758) sin 11° au = 0,57 au
Situácia je v skutočnosti zložitejšia (nezahrnuli sme napr. natočenie obežnej trajektórie v priestore, predpokladali sme, že príslnie a odslnie sa nachádzajú najďalej od ekliptiky), presnejšie výpočty však výrazne prevyšujú znalosti na úrovni základnej školy, preto sa uspokojíme aspoň s týmto približným výpočtom.
Úloha: Trpasličia planéta Ceres má polomer 457 km. V Bratislave jazdí autobus s dĺžkou 25 metrov. Koľko autobusov sa vojde do priemeru trpasličej planéty Ceres?
Riešenie: Priemer Ceres = 2 ∙ polomer Ceres = 2 ∙ 457 km = 914 km = 914 000 m. Dĺžka autobusu = 25 m. Počet autobusov n = 914 000/25 = 36 560 ks. Do priemeru Ceres sa vojde viac ako 36 500 autobusov.
Úloha: V tejto časti sa pokúsime odhadnúť obežnú rýchlosť trpasličej planéty, ktorá sa nachádza v hlavnom páse planétok. Pre jednoduchosť budeme uvažovať, že sa objekt pohybuje po kruhovej obežnej trajektórii.
a) Ceres, skôr išlo o najväčšiu planétku v hlavnom páse planétok, teraz ide o trpasličiu planétu, obehne okolo Slnka raz za 4,6 roka. Vypočítaj, koľko sekúnd trvá trpasličej planéte Ceres, kým dokončí jeden obeh.
Riešenie: 1 rok = 365 dní ∙ 24 hodín ∙ 60 minút ∙ 60 sekúnd = 31 536 000 s. Jeden obeh Ceres okolo Slnka trvá 4,6 ∙ 31 536 000 s = 145 miliónov sekúnd. Bolo by možné použiť aj dĺžku tropického roka (čas medzi dvoma po sebe nasledujúcimi priechodmi pravého Slnka – stredu slnečného disku – jarným bodom), ktorý trvá 31 556 925 s, avšak výsledný počet sekúnd zaokrúhlený na milióny sekúnd sa nezmení.
b) Ceres sa nachádza vo vzdialenosti 2,77 au od Slnka. 1 au je 150 miliónov km. Vypočítaj vzdialenosť trpasličej planéty Ceres od Slnka v km.
Riešenie: Ceres sa nachádza vo vzdialenosti 2,77 ∙ 150 000 000 km = 416 miliónov km.
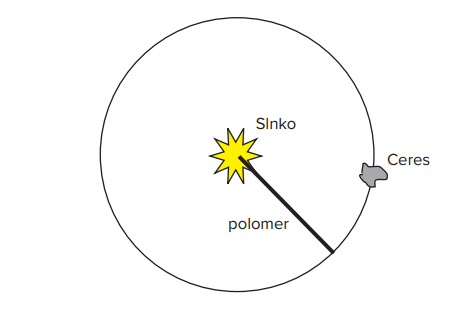
c) Predpokladajme, že Ceres obieha okolo Slnka po kruhovej dráhe. Nakresli schematický obrázok, ktorý bude znázorňovať obežnú trajektóriu trpasličej planéty. Na obrázku znázorni a označ Slnko, Ceres a polomer kružnice (obežnej trajektórie).
Riešenie:
d) Použi vzdialenosť z časti b) a vypočítaj, koľko km prejde Ceres pri jednom obehu. (Pomôcka: obvod kruhu sa vypočíta pomocou vzťahu , kde
3,14)
Riešenie: Obvod obežnej trajektórie km = 2,6 miliardy km.
Pre porovnanie možno uviesť, že dĺžka obežnej trajektórie Zeme je necelá jedna miliarda kilometrov.
e) Použi vzťah pre výpočet priemernej rýchlosti v = s / t a použitím odpovedí v častiach a) a b) vypočítaj, akou rýchlosťou sa Ceres pohybuje okolo Slnka.
Riešenie: Priemerná rýchlosť Ceres okolo Slnka je v = s / t = 2,6 ∙ 109 / 145 ∙ 106 km · s–1 = 17,9 km · s–1. Pre porovnanie, Zem sa na svojej obežnej trajektórii pohybuje priemernou rýchlosťou 30 km s–1.
Úloha: obežná rýchlosť trpasličej planéty Pluto
a) Pluto, skôr išlo o planétu, teraz ide o trpasličiu planétu, obehne okolo Slnka raz za 248 rokov. Vypočítaj, koľko sekúnd trvá trpasličej planéte Pluto, kým dokončí jeden obeh.
Riešenie: Jeden obeh trpasličej planéty Pluto okolo Slnka trvá 248 ∙ 31 536 000 s = 7,8 miliardy sekúnd. Bolo by možné použiť aj dĺžku tropického roka, avšak výsledný počet sekúnd zaokrúhlený na desatiny miliárd sekúnd sa nezmení.
b) Vypočítaj, koľkokrát Pluto obehlo okolo Slnka od svojho objavu v roku 1930.
Riešenie: Pluto svoj obeh okolo Slnka od svojho objavenia dokončí až v roku 2178, takže zatiaľ od svojho objavu neobehlo okolo Slnka ani raz. Od svojho objavu Pluto (k roku 2019) prešlo 36 % celkovej obežnej trajektórie. (2019 – 1930) / 248 = 0,36.
c) Pluto sa nachádza v priemernej vzdialenosti 39,5 au od Slnka. 1 au je 150 miliónov km. Vypočítaj vzdialenosť trpasličej planéty Pluto od Slnka v km.
Riešenie: Pluto sa nachádza vo vzdialenosti 39,5 ∙ 150 000 000 km = 5,9 miliónov km.
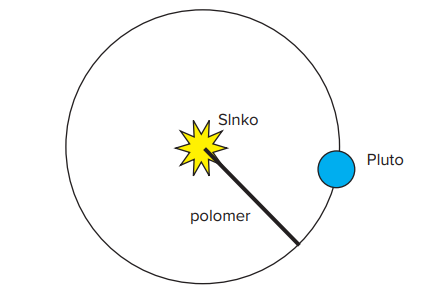
d) Predpokladaj, že Pluto obieha okolo Slnka po kruhovej dráhe. Nakresli schematický obrázok, ktorý bude znázorňovať obežnú trajektóriu trpasličej planéty. Na obrázku znázorni a označ Slnko, Pluto a polomer kružnice (obežnej trajektórie).
Riešenie:
e) Použi vzdialenosť z časti c) a vypočítaj, koľko km prejde Pluto pri jednom obehu. (Pomôcka: obvod kruhu sa vypočíta pomocou vzťahu , kde
3,14)
Riešenie: Riešenie: Obvod obežnej trajektórie km = 37 miliard km. Pre porovnanie možno uviesť, že Zem prejde na svojej obežnej trajektórii okolo Slnka necelú jednu miliardu kilometrov. Pluto sa v skutočnosti nepohybuje po kružnici, ale po elipse s výstrednosťou 0,25. Vzorec na výpočet obvodu elipsy presahuje náročnosťou učivo základnej školy. Chyba určenia obvodu elipsy pri použití vzorca pre obvod kruhu je v ráde niekoľkých percent, na tento účel je teda náhrada obvodom kruhu dostatočná.
f) Použi vzťah pre výpočet priemernej rýchlosti v = s / t a použitím odpovedí v častiach a) a e), vypočítaj, akou rýchlosťou sa Pluto pohybuje okolo Slnka.
Riešenie: Priemerná rýchlosť Pluto okolo Slnka je v = s / t = 37 ∙ 109 / 7,8 ∙ 109 km · s–1 = 4,7 km · s–1. Pre porovnanie, Mesiac sa na svojej obežnej trajektórii okolo Zeme pohybuje priemernou rýchlosťou 1 km s–1.
Úloha: Kedy bude Ceres zapadať? V tejto úlohe budeme predpovedať, kedy zapadne trpasličia planéta Ceres, pokiaľ ju budeme pozorovať pomocou ďalekohľadu Faulkes Telescope North (FTN) na Havaji. Predpokladajme, že západ objektu je okamih, kedy bude vo výške 0° nad obzorom.
Nižšie uvedená tabuľka obsahuje výšku Ceres nad obzorom, ako bola vidieť z FTN, pre každý deň po dobu 21 dní od 27. 2. 2006. Na prvý pohľad je z dát zrejmé, že sa výška Ceres nad obzorom každým dňom postupne znižuje. Kedy dosiahne horizont?
| Deň | Výška nad obzorom (°) | Deň | Výška nad obzorom (°) |
| 1 | 19 | 12 | 14 |
| 2 | 19 | 13 | 14 |
| 3 | 18 | 14 | 13 |
| 4 | 18 | 15 | 13 |
| 5 | 17 | 16 | 12 |
| 6 | 17 | 17 | 12 |
| 7 | 16 | 18 | 11 |
| 8 | 16 | 19 | 11 |
| 9 | 16 | 20 | 10 |
| 10 | 15 | 21 | 10 |
| 11 | 15 |
a) Nakresli graf závislosti výšky Ceres nad obzorom od dní, pričom použi dáta z vyššie uvedenej tabuľky. Nakreslenými bodmi prelož priamku.
Riešenie:
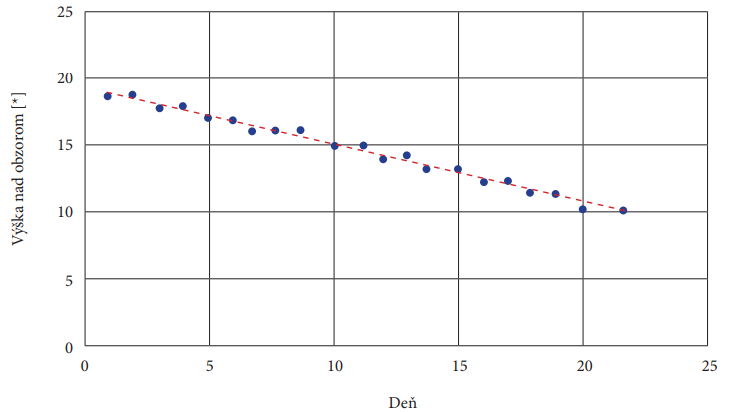
b) Vypočítaj sklon priamky a jej priesečník s osou y. Za predpokladu, že najlepšie možno body preložiť priamkou, aká je rovnica pre tieto dáta?
Riešenie: Medzi 1. a 21. dňom (20 dní) je rozdiel výšky (klesne o) 9°, tzn. sklon priamky je 9° / 20 = –0,45°. Priesečník s osou y je 19. Rovnica priamky je v tvare y = −0,45x + 19.
c) Urči, za koľko dní bude Ceres pod obzorom. (Pomôcka: Objekt zapadne, ak je jeho výška nad obzorom 0°.)
Riešenie: Západ Ceres je okamih, kedy je výška nad obzorom 0°, tzn. y = 0. Riešime rovnicu a hľadáme x, pre ktoré platí, že y je rovné 0. Môžeme písať
0,45x = 19
x = 42
Ceres zapadne za 42 dní.
Úloha: Obežná trajektória trpasličej planéty Pluto je odlišná od obehových trajektórií planét – výstrednosť 0,25, sklon 17°. Výstrednosť trajektórií planét sa pohybuje od 0,007 (Venuša) až 0,206 (Merkúr), pričom väčšina planét má výstrednosť menšiu ako 0,1. Sklon obežnej trajektórie voči rovine ekliptiky je u planét v rozsahu 0° (Zem, z definície ekliptiky) až po 7° (Merkúr). Vďaka tomu sa Pluto dostáva v malom úseku (od 7. 2. 1979 až po 11. 2. 1999) svojej trajektórie k Slnku bližšie ako Neptún, keď si jeho obežnú trajektóriu premietneme do roviny ekliptiky.
a) Predpokladaj, že sa Pluto pohybuje po kruhovej obežnej trajektórii. Vypočítaj, koľko percent času sa Pluto nachádza k Slnku bližšie ako planéta Neptún? Koľko je to dní?
Riešenie: Obežná doba Pluta je 248 rokov. Pluto je bližšie medzi rokmi 1979 až 1999, čo je 20 rokov. S ohľadom na presnosť výpočtu postačí počítanie na úrovni rokov, takže 20 : 248 = 8 %. Medzi 7. 2. 1979 až 11. 2. 1999 uplynie 7 309 dní = 20 rokov · 365 dní + 5 dní za prestupné roky (1980, 1984, 1988, 1992 a 1996) + 4 dni (od 7. dňa v mesiaci do 11. dňa v mesiaci).
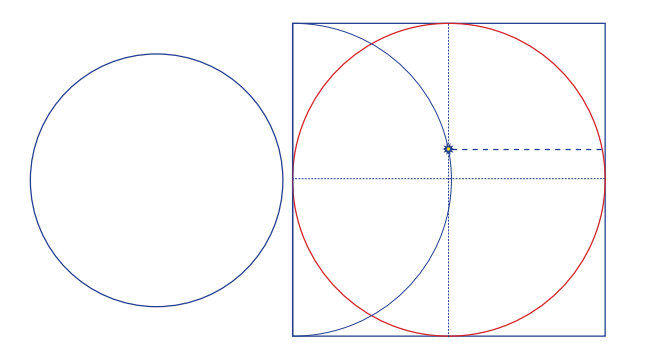
b) Na modeli trajektórií Neptúna a Pluta sa presvedč, že sa Neptún s Plutom nemôžu zraziť. Vyrob si jednoduchý model trajektórií planéty Neptún a trpasličej planéty Pluto. Na list papiera formátu A4 narysuj kružnicu s polomerom 7,5 cm, ktorá bude predstavovať obežnú trajektóriu Neptúna. Vytvorený kruh vystrihni a na jednom mieste prestrihni až do stredu kružnice. Na ďalší list papiera si vytvoríš trajektóriu Pluta, bude lepšie, ak si na počítači v nejakom programe (napr. možné aj v textovom editore) nakreslíš obdĺžnik so stranami 19,8 cm a 19,2 cm. Do neho nakreslíš elipsu, aby sa dotýkala všetkých strán obdĺžnika. Vyznač bodkočiarkovane obe osi elipsy. Polohu Slnka získaš tak, že nakreslíš polkružnicu okolo stredu dlhšej strany obdĺžnika s priemerom 19,8 cm a nájdeš priesečník s dlhšou osou elipsy. Nakoniec zostroj kolmicu k dlhšej osi elipsy tak, aby prechádzala Slnkom. Obrázok vytlač v správnej mierke na formát A4, trajektóriu vystrihni vrátane vyznačenej kolmice. Obidva modely trajektórií do seba zasuň tak, aby zvierali uhol 17°.
Úloha: Koľko vážiš, závisí od gravitačnej sily v mieste, kde sa nachádzaš. Nižšie uvedená tabuľka ukazuje, aká by bola gravitačná sila na rôznych miestach v slnečnej sústave v porovnaní s hodnotou (1,00) na zemskom povrchu. Pokiaľ na Zemi niekto váži 100 kg, na Mesiaci by vážil 17 kg. K tejto hodnote sa dospeje nasledujúcim spôsobom: 100 kg („váha“ na Zemi) vynásobených 0,17 (gravitačný faktor pre Mesiac) = 17 kg. Je potrebné si uvevdomiť, že hmotnosť sa na rôznych miestach nemení, zostáva stále rovnaká. Iba sa mení ťarcha, ktorá súvisí s gravitačnou silou.
Tvoja hmotnosť na Zemi: _ _ _ _ _ _ _ _ _ _ kg
| Miesto | Gravitačný faktor na povrchu (Zeme = 1,00) |
Moja „váha“ na tomto mieste |
| Slnko | 28 | 2 800 |
| Merkúr | 0,38 | 38 |
| Venuša | 0,9 | 90 |
| Zem | 1,0 | 100 |
| Mesiac | 0,17 | 17 |
| Mars | 0,38 | 38 |
| Ceres | 0,029 | 2,9 |
| Jupiter | 2,53 | 253 |
| Saturn | 1,1 | 110 |
| Urán | 0,9 | 90 |
| Neptún | 1,14 | 114 |
| Pluto | 0,06 | 6 |
Je potrebné si uvedomiť, že na plynných planétach a Slnku nemožno v skutočnosti pristáť, pretože nemajú pevný povrch. Zoraď zoznam miest podľa toho, kde je tvoja „váha“ najväčšia po najmenšiu. Od akého parametra závisí zmena tvojej „váhy“?
Riešenie: Slnko, Jupiter, Neptún, Saturn, Zem, Venuša, Urán, Merkúr, Mars, Mesiac, Pluto, Ceres. Zmena závisí od gravitačného faktora, ktorý je ovplyvnený hmotnosťou objektu, jeho rozmerom (gravitačná sila) a dobou rotácie okolo osi, rozmermi objektu (odstredivá sila).
Úloha: V tejto úlohe si vyskúšame, ako hmotnosť planéty ovplyvňuje skok do výšky.
Postup:
1. Žiaci vytvoria skupiny po troch.
2. Jeden žiak zo skupiny drží metrové pravítko zvislo k podlahe, pričom začiatok stupnice pravítka sa dotýka podlahy.
3. Druhý žiak zo skupiny pozoruje stupnicu pravítka a zaznamená výšku výskoku tretieho žiaka zo skupiny.
4. Tretí žiak zo skupiny vyskočí do výšky vedľa pravítka. Výška výskoku je zaznamenaná a opakovaná celkom trikrát. Z troch výšok sa vypočíta priemerná výška výskoku, ktorá sa zaznamená do formulára a bude považovaná za výšku výskoku na Zemi.
5. Žiaci si medzi sebou vymenia roly, to znamená, že každý bude skokanom a zaznamená sa u neho priemerná výška výskoku na Zemi.
Tabuľka 1: Výpočet priemernej výšky výskoku na Zemi
| Výskok | Pokus #1 | Pokus #2 | Pokus #3 | Priemerný výskok |
| Výška (cm) | 53 | 50 | 47 | 50 |
6. Pomocou Tabuľky 2 vypočítaj priemernú výšku výskoku na iných miestach v slnečnej sústave.
7. Doplň Tabuľku 3 tým, že vypíšeš planéty, Slnko a trpasličiu planétu Pluto a výšku tvojho výskoku podľa hmotnosti objektu od najmenej hmotného objektu až po najhmotnejší objekt.
8. Vytvor stĺpcový graf výšky výskoku, pričom poradie objektov je vzostupne podľa hmotnosti objektu.
Tabuľka 2: Ako výšku výskoku ovplyvňuje hmotnosť objektu slnečnej sústavy
| Objekt | Hmotnosť objektu slnečnej sústavy (× 1023 kg) |
Priemerná výška výskoku na Zemi (cm) |
Prepočítavací koeficient pre výšku výskoku |
Výška výskoku na objekte (cm) |
| Slnko | 19 900 000 | 50 | ×0,036 | 1,8 |
| Merkúr | 3,3 | 50 | ×2,63 | 132 |
| Venuša | 48,7 | 50 | ×1,11 | 55,5 |
| Zem | 59,7 | 50 | ×1 | 50 |
| Mesiac | 0,73 | 50 | ×5,88 | 294 |
| Mars | 6,42 | 50 | ×2,63 | 132 |
| Ceres | 0,0094 | 50 | ×34,5 | 1 730 |
| Jupiter | 19 00 | 50 | ×0,40 | 20 |
| Saturn | 5 680 | 50 | ×0,91 | 46 |
| Urán | 868 | 50 | ×1,11 | 55,5 |
| Neptún | 1 020 | 50 | ×0,88 | 44 |
| Pluto | 0,13 | 50 | ×16,7 | 835 |
Použi vyššie uvedené hmotnosti na zoradenie objektov slnečnej sústavy od najmenej hmotného po najhmotnejší a zapíš do nižšie uvedenej tabuľky. Zapíš do tabuľky aj výšku výskoku u každého vypísaného objektu slnečnej sústavy.
Tabuľka 3: Poradie objektov slnečnej sústavy podľa hmotnosti
| Objekt slnečnej sústavy | Výška výskoku na danom objekte |
| Slnko | 1 730 |
| Merkúr | 835 |
| Venuša | 294 |
| Zem | 132 |
| Mesiac | 132 |
| Mars | 55,5 |
| Ceres | 50 |
| Jupiter | 5,55 |
| Saturn | 44 |
| Urán | 46 |
| Neptún | 20 |
| Pluto | 1,8 |
Použi dáta z tabuliek vyššie a vytvor stĺpcový alebo čiarový graf, ktorý porovná hmotnosti objektov slnečnej sústavy a výšku tvojho výskoku. Na vodorovnej osi zoraď objekty od najmenej hmotného po najhmotnejší.
Riešenie
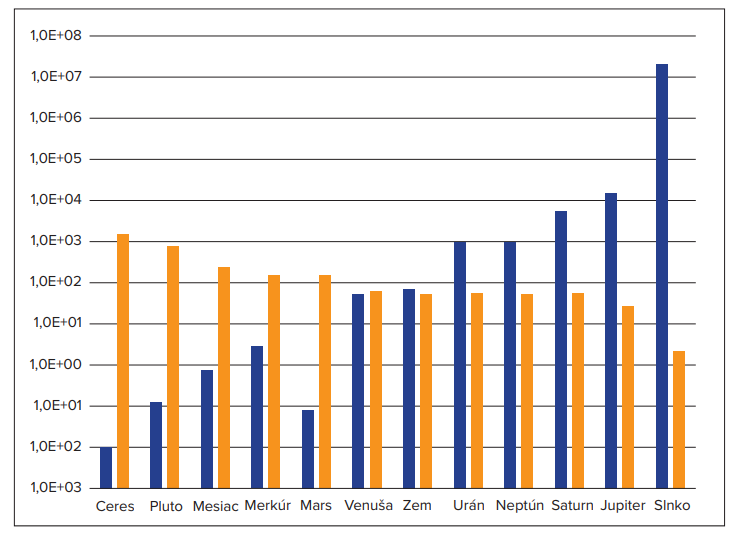
Úloha: Na ktorom objekte slnečnej sústavy možno vyskočiť najviac, na ktorom je možné vyskočiť najmenej?
Riešenie: Najvyššie je možné vyskočiť na trpasličej planéte Ceres, najmenej na Slnku, avšak tento objekt nemá pevný povrch, ako v poradí ďalšie plynné planéty. Takže by za správnu odpoveď mohla byť považovaná Zem.
Úloha: Prečo je možné vyskočiť vyššie na Merkúre než na Neptúne?
Riešenie: Na Merkúre na nás pôsobí menšia gravitačná (resp. tiažová) sila, preto tu môžeme vyskočiť vyššie. Je vhodné upozorniť, že Neptún je plynná planéta a nemá pevný povrch.
Úloha: Ak by si chcel/a prekonať svetový rekord v skoku do výšky, aký objekt slnečnej sústavy by si vybral/a? Prečo? Na akých objektoch slnečnej sústavy by si už prekonal/a existujúci svetový rekord v skoku do výšky?
Riešenie: Vybral/a by som trpasličiu planétu Ceres alebo Pluto, vzhľadom na ich vzdialenosti od Zeme by som radšej preferoval Mesiac, ktorý je od Zeme približne 384 tisíc km. Rekord by sa dal prekonať na ostatných kamenných planétach, tzn. na Merkúre, na Venuši aj na Marse.