- Úloha 1 Radiány, alebo stupne?
- Úloha 2 Mars v opozícii a kvadratúre
- Úloha 3 MERIAME MERKÚR A VENUŠU
- Úloha 4 „MERKUAN“
- Úloha 5 Zem z Marsu
- Úloha 6 Aký veľký je mesiac?
- Úloha 7 Mesiac druhýkrát
- Úloha 8 Parametre trajektórie planét
- Úloha 9 Ako z inej planéty...
- Úloha 10 Nohami pevne na Zemi...
- Úloha 11 Grék, aká veľká je zem?
- Úloha 12 MESIAC V AKCII PO TRETIE
Úloha 6: Aký veľký je mesiac?
a) Stredná vzdialenosť Zem – Slnko je d = 1 au = 1,496 ⋅ 108 km, polomer Slnka je d = 1 au = 1,496 ⋅ 108 km, polomer Slnka je R☉ = 6,955 ⋅ 105 km. Určte uhlovú veľkosť Slnka pre pozorovateľa na Zemi.
b) Zo znalosti hmotnosti Zeme M⊕ = 5,97 ⋅ 1024 kg a doby obehu Mesiaca okolo Zeme M⊕ = 5,97 ⋅ 1024 kg a doby obehu Mesiaca okolo Zeme T = 27,3 dní odhadnite z tretieho Keplerovho zákona vzdialenosť Mesiaca od Zeme. Hmotnosť Mesiaca pre odhad vzdialenosti neberte do úvahy.
c) Pretože viete, že dochádza k čiastočným aj úplným zatmeniam Slnka, odhadnite skutočné rozmery Mesiaca. Ilustrácia javu je na Obr. 2.

Obrázok 2: Zdroj: https://apod.nasa.gov/
apod/ap160831.html, cit. 5.8.2018

Obrázok 3: Zdroj: https://www.nasa.gov/multimedia/
imagegallery/image_feature_1249.html, cit. 5.8.2018
d) Aká by bola uhlová veľkosť Zeme pre astronauta na Mesiaci, keď by sa Mesiac pohyboval po presne kruhovej dráhe? Akú veľkú časť povrchu Zeme astronaut vidí (pozri Obr. 3 a 4)? Výsledok vyjadrite v percentách. Polomer Zeme je R⊕ = 6 378 km.
Pomôcka: Časť povrchu Zeme, ktorú pozorovateľ vidí, zodpovedá povrchu guľového vrcholíka. Plocha guľového vrcholíka (bez podstavy) je , kde
, kde R je polomer sféry
, kde R je polomer sféry a v je výška guľovej úseče, pozri Obr. 4.
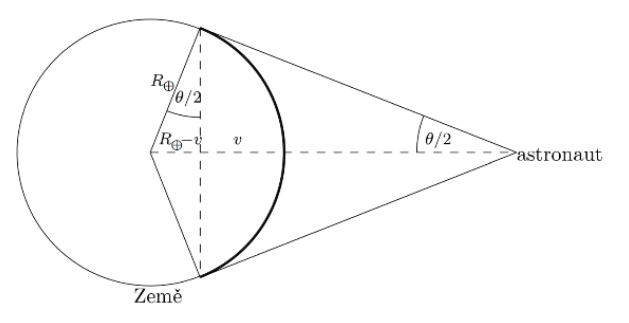
Obrázok 4: Ilustrácia pohľadu astronauta na Zem
Riešenie
a) Vyjdeme z približného vzťahu pre uhlovú veľkosť:.
Mohli by sme vyjsť aj z presného vzťahu
Mohli by sme vyjsť aj z presného vzťahu
resp.
.
Mohli by sme vyjsť aj z presného vzťahu tg tg . Výsledky sú samozrejme rovnaké, pozri Úloha I.
b) Vyjdeme z 3. Keplerovho zákona: .
c) Pretože dochádza k čiastočným a úplným zatmeniam Slnka, je uhlová veľkosť Mesiaca porovnateľná s uhlovou veľkosťou Slnka, teda . Polomer Mesiaca určíme zo vzťahu:
. Polomer Mesiaca určíme zo vzťahu:
. Skutočný polomer Mesiaca je 1 737 km, teda náš výsledok súhlasí dobre so skutočnosťou.
d) Vyjdeme z približného vzťahu pre uhlovú veľkosť: .
Z Obr. 2 zjavne platí: . Z Obr. 2 zjavne platí:
. Z obr. 2 zjavne platí:
.
Buď môžeme výšku guľového vrchlíka spočítať priamo zo zadaných hodnôt, alebo z vypočítanej hodnoty uhlovej veľkosti Zeme. Dosadíme do pomocného vzorca pre plochu guľového vrcholíka . Z Obr. 2 zjavne platí:
.
Buď môžeme výšku guľového vrcholíka spočítať priamo zo zadaných hodnôt, alebo z vypočítanej hodnoty uhlovej veľkosti Zeme. Dosadíme do pomocného vzorca pre plochu guľového vrcholíka
. Vzorec pre plochu gule je
.
Z obr. 2 zjavne platí:
.
Buď môžeme výšku guľového vrcholíka spočítať priamo zo zadaných hodnôt, alebo z vypočítanej hodnoty uhlovej veľkosti Zeme. Dosadíme do pomocného vzorca pre plochu guľového vrcholíka
. Vzorec pro plochu gule je
, preto pre pomer plochy guľového vrcholíka k celej guli je:
.Z Obr. 2 zjavne platí:
.
Buď môžeme výšku guľového vrcholíka spočítať priamo zo zadaných hodnôt, alebo z vypočítanej hodnoty uhlovej veľkosti Zeme. Dosadíme do pomocného vzorca pre plochu guľového vrcholíka
. Vzorec pro plochu gule je
, preto pre pomer plochy guľového vrcholíka k celej guli je:
.Astronaut vidí takmer celú jednu stranu Zeme.
Z poslednej rovnice je jasné, že čím bude astronaut ďalej od Zeme (vzdialenosť pritom udáva hlavná polos, pretože zodpovedá polomeru kruhového orbitu), tým bude člen
. Z Obr. 2 zjavne platí:
.
. Vzorec pre plochu gule je
, preto pre pomer plochy guľového vrcholíka k celej guli je:
.
Astronaut vidí takmer celú jednu stranu Zeme. Z poslednej rovnice je jasné, že čím bude astronaut ďalej od Zeme (vzdialenosť pritom udáva hlavná polos, pretože zodpovedá polomeru kruhového orbitu), tým bude člen bližšie nule a astronaut uvidí väčšiu časť Zeme, maximálne však
. Z obr. 2 zjavne platí:
. Buď môžeme výšku guľového vrcholíka spočítať priamo zo zadaných hodnôt, alebo z vypočítanej hodnoty uhlovej veľkosti Zeme. Dosadíme do pomocného vzorca pre plochu guľového vrcholíka
. Vzorec pre plochu gule je
, preto pre pomer plochy guľového vrcholíka k celej guli je:
. Astronaut vidí takmer celú jednu stranu Zeme. Z poslednej rovnice je jasné, že čím bude astronaut ďalej od Zeme (vzdialenosť pritom udáva hlavná polos, pretože zodpovedá polomeru kruhového orbitu), tým bude člen
bližšie nule a astronaut uvidí väčšiu časť Zeme, maximálne však 50 %. Ak bude astronaut naopak tesne nad povrchom Zeme, bude člen
. Z Obr. 2 zjavne platí:
. Buď môžeme výšku guľového vrcholíka spočítať priamo zo zadaných hodnôt, alebo z vypočítanej hodnoty uhlovej veľkosti Zeme. Dosadíme do pomocného vzorca pre plochu guľového vrcholíka
. Vzorec pre plochu gule je
, preto pre pomer plochy guľového vrcholíka k celej guli je:
. Astronaut vidí takmer celú jednu stranu Zeme. Z poslednej rovnice je jasné, že čím bude astronaut ďalej od Zeme (vzdialenosť pritom udáva hlavná polos, pretože zodpovedá polomeru kruhového orbitu), tým bude člen
bližšie nule a astronaut uvidí väčšiu časť Zeme, maximálne však 50 %. Ak bude astronaut naopak tesne nad povrchom Zeme, bude člen
blízko 1 a pomer
. Z obr. 2 zjavne platí:
. Buď môžeme výšku guľového vrcholíka spočítať priamo zo zadaných hodnôt, alebo z vypočítanej hodnoty uhlovej veľkosti Zeme. Dosadíme do pomocného vzorca pre plochu guľového vrcholíka
. Vzorec pre plochu gule je
, preto pre pomer plochy guľového vrcholíka k celej guli je:
. Astronaut vidí takmer celú jednu stranu Zeme. Z poslednej rovnice je jasné, že čím bude astronaut ďalej od Zeme (vzdialenosť pritom udáva hlavná polos, pretože zodpovedá polomeru kruhového orbitu), tým bude člen
bližšie nule a astronaut uvidí väčšiu časť Zeme, maximálne však 50 %. Ak bude astronaut naopak tesne nad povrchom Zeme, bude člen
blízko 1 a pomer
bude takmer nulový.