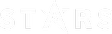Задача 2: Планетите-джуджета и техните траектории
Задача: Определете разстоянията на планетите- джуджета в перихелий и в афелий. Подредете планетите-джуджета във възходящ ред според разстоянието, на което се намират от Слънцето в перихелий и в афелий. Изчислете за всеки един космически обект сумата от разстоянията в перихелий и в афелий. Сравнете получената стойност с голямата полуос, умножена по две.
(Съвет: Разстоянието в перихелий е a(1 – e), а в афелий е a(1 + e).)
Решение:
| Име | Голяма полуос a (au) |
Ексцентричност на траекторията e (–) |
Разстояние в перихелий rP (au) |
Разстояние в афелий rP (au) |
rP + rA (au) |
2a (au) |
| Церера | 2,77 | 0,0758 | 2,56 | 2,98 | 5,54 | 5,54 |
| Плутон | 39,5 | 0,2488 | 29,7 | 49,3 | 79 | 79 |
| Хаумея | 43,2 | 0,191 | 34,9 | 51,5 | 86,4 | 86,4 |
| Макемаке | 45,7 | 0,156 | 38,6 | 52,8 | 91,4 | 91,4 |
| Ерида | 67,8 | 0,441 | 37,9 | 97,7 | 135,6 | 135,6 |
Повечето космически обекти от Слънчевата система се движат извън еклиптичната равнина, в която Земята обикаля около Слънцето. Орбиталната равнина на дадено тяло сключва с еклиптичната равнина ъгъл, който обозначаваме с i, от думата „инклинация“ (наклон на траекторията). Нека разгледаме влиянието на наклона на орбиталната равнина на даден обект. За този случай ще ни трябват тригонометричните функции на синус и косинус.
Задача: Определете разстоянията на планетите-джуджета в перихелий и в афелий, като ги проектирате в еклиптичната равнина и включете наклона на орбиталните им траектории. На какво разстояние от еклиптичната равнина се намират планетите- джуджета, ако са в перихелий или в афелий.
Решение:
| Име |
Голяма полуос a (au) |
Ексцентричност на траекторията e (-) |
Наклон на траекторията i (°) |
Разстояние в перихелий в еклиптичната равнина (au) |
Разстояние в афелий в еклиптичната равнина (au) |
Разстояние от еклиптиката в перихелий (au) |
Разстояние от еклиптиката в афелий (au) |
| Церера | 2,77 | 0,0758 | 11 | 2,51 | 2,93 | 0,49 | 0,57 |
| Плутон |
39,5 | 0,2488 | 17 | 28,4 | 47,1 | 8,7 | 14,4 |
| Хаумея |
43,2 | 0,191 | 28 | 30,8 | 45,5 | 16,4 | 24,2 |
| Макемаке |
45,7 | 0,156 | 29 | 33,8 | 46,2 | 18,7 | 25,6 |
| Ерида |
67,8 | 0,441 | 44 | 27,3 | 70,3 | 26,3 | 67,9 |
Разстояние в перихелий в еклиптичната равнина (за Церера):
a (1 – e) cos i = 2,77 (1 – 0,0758) cos 11° au = 2,51 au
Разстояние в афелий в еклиптичната равнина (за Церера):
a (1 + e) cos i = 2,77 (1 + 0,0758) cos 11° au = 2,93 au
Разстояние от еклиптиката в перихелий (за Церера):
a (1 – e) sin i = 2,77 (1 – 0,0758) sin 11° au = 0,49 au
Разстояние от еклиптиката в афелий (за Церера):
a (1 + e) sin i = 2,77 (1 + 0,0758) sin 11° au = 0,57 au
Ситуацията всъщност е много по-сложна (тук не сме включили например наклона на орбиталната траектория в пространството, предположили сме, че перихелият и афелият се намират извън еклиптиката), но по-точни изчисления далеч надхвърлят уменията от училище, следователно ще приемем поне тези приблизителни изчисления.
Задача: Планетата-джудже Церера има радиус от 457 km. В Братислава има автобуси с дължина от 25 метра. Колко автобуса се вписват в радиуса на планетата-джудже Церера?nbsp;
Решение: Диаметър на Церера = 2 ∙ Радиус на Церера = 2 ∙ 457 km = 914 km = 914 000 m. Дължина на автобуса = 25 m. Брой на автобусите n = 914 000/25 = 36 560 броя. Следователно, в диаметъра на Церера ще се съберат повече от 36 500 автобуса.
Задача: В тази част ще се опитаме да определим орбиталната скорост на планетата- джудже, която е разположена в Главния астероиден пояс. За по-лесно ще считаме, че космическият обект се движи по кръгова орбита.
а) Церера, някога най-голямата малка планета в Главния астероиден пояс, а сега – планета-джудже, се завърта около Слънцето веднъж на 4,6 години. Изчислете колко секунди са необходими на планетата-джудже Церера, за да направи едно пълно завъртане.
Решение: 1 година = 365 дни ∙ 24 часа ∙ 60 минути ∙ 60 секунди = 31 536 000 секунди (s). Едно завътртане на Церера около Слънцето трае 4,6 ∙ 31 536 000 s = 145 милиона секунди. Също така би било възможно да се използва продължителността на тропическата година (времето между два последователни преминавания на истинското Слънце – центърът на слънчевия диск – през пролетната равноденствена точка), което продължава 31 556 925 s, но полученият брой секунди, закръглени до милиони секунди, остава непроменен.
б) Церера е разположена на разстояние 2,77 астрономически единици (au) от Слънцето. 1 au е 150 милиона км. Изчислете разстоянието на планетата-джудже Церера от Слънцето в км.
Решение: Церера се намира на 2,77 ∙ 150 000 000 km = 416 000 000 km.
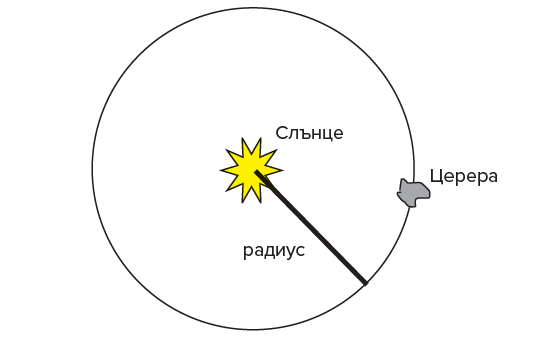
в) Да предположим, че Церера обикаля около Слънцето по кръгова орбита. Начертайте схематично изображение, което да илюстрира орбиталната траектория на планетата-джудже. На фигурата отбележете положението на Слънцето, Церера и радиуса на окръжността (орбиталната траектория).
Решение:
г) Използвайте разстоянието от част б) и изчислете колко километра ще измине Церера при една своя обиколка? (Съвет: Обиколката на окръжността се изчислява, като се използва отношението o = 2πr, където r е радиусът на окръжността)
Решение: Обиколка на орбитата е o = 2πr = 2π ∙ 416 ∙ 106 km = 2,6 милиарда км.
За сравнение, дължината на орбитата на Земята е по-малка от един милиард километра.
д) Използвайте тази връзка, за да изчислите средната скорост v = s / t и използвайте отговорите от части а) и б), за да изчислите скоростта, с която Церера се движи около Слънцето.
Решение: Средната скорост на Церера около Слънцето е v = s / t = 2,6 ∙ 109 / 145 ∙ 106 km · s–1 = 17,9 km · s–1. За сравнение, Земята се движи по своята орбита със средна скорост от 30 km ∙ s–1.
Задача: Орбитална скорост на планетата-джудже Плутон
а) Плутон, която е планета-джудже, се завърта около Слънцето веднъж на 248 години. Изчислете колко секунди са необходими на планетата-джудже Плутон, за да направи едно пълно завъртане.
Решение: Една обиколка на планетата-джудже Плутон около Слънцето отнема 248 ∙ 31 536 000 s = 7,8 милиарда секунди. Тропическата година също може да се използва, но полученият брой секунди, закръглени до десети от милиарда секунди, няма да се промени.
б) Изчислете колко пъти Плутон е обиколил Слънцето от откриването си през 1930 г.
Решение: Плутон ще завърши обикалянето си около Слънцето чак през 2178 г., така че от откриването си до сега не е направил дори една пълна обиколка около Слънцето. От откриването на Плутон (към 2019 г.) той е изминал 36% от общата си орбита. (2019 – 1930) / 248 = 0,36.
в) Плутон е разположен на средно разстояние от 39,5 au от Слънцето. 1 au е 150 милиона км. Изчислете разстоянието на планетата-джудже Плутон от Слънцето в км.
Решение: Плутон се намира на разстояние 39,5 ∙ 150 000 000 km = 5,9 милиона км.
г) Да предположим, че Плутон обикаля около Слънцето по кръгова орбита. Начертайте схематично изображение, което да илюстрира орбиталната траектория на планетата-джудже. На фигурата отбележете положението на Слънцето, Плутон и радиуса на окръжността (орбиталната траектория).
Решение:

д) Използвайте разстоянието от част б) и изчислете колко километра ще измине Плутон при една обиколка. (Съвет: Обиколката на окръжността се изчислява, като се използва отношението o = 2πr, където r е радиусът на окръжността)
Решение: Орбиталната обиколка е o = 2πr = 2π ∙ 5,9 ∙ 109 km = 37 милиарда км. За сравнение, Земята ще измине по-малко от един милиард километра по своята орбита около Слънцето. Всъщност Плутон не се движи по окръжност, а по елипса с ексцентрицитет 0,25. Формулата за изчисляване на обиколката на елипса надхвърля учебната програма на началното училище. Грешката при определяне на обиколката на елипса с помощта на формулата за обиколката на окръжността е от порядъка на няколко процента, така че замяната с обиколката на окръжността е достатъчна за целта на помагалото.
е) Използвайте формулата, за да изчислите средната скорост v = s / t и използвайте отговорите в части а) и д), за да изчислите скоростта, с която Плутон се движи около Слънцето.
Решение: Средната скорост на Плутон около Слънцето е v = s / t = 37 ∙ 109 / 7,8 ∙ 109 km · s–1 = 4,7 km · s–1. За сравнение, Луната се движи със средна скорост от 1 km · s–1 по своята орбита около Земята.
Задача: Кога ще залязва Церера? В тази задача ще прогнозираме кога планетата- джудже Церера ще залезе, ако я наблюдаваме с телескопа Фолкс Север (Faulkes Telescope North (FTN)), намиращ се на Хавайските острови. Да предположим, че залязването на космическия обект става в момента, в който той се намира на височина от 0 ° над хоризонта.
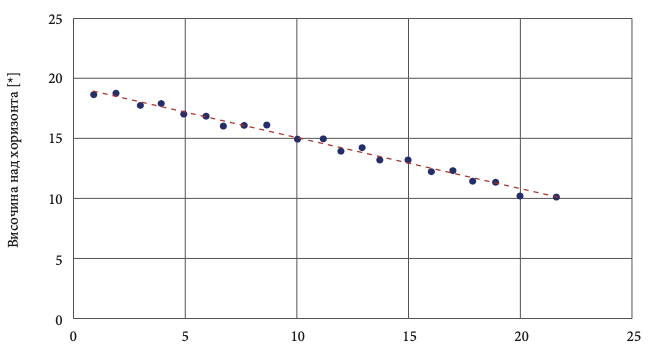
Таблицата по-долу показва височината на Церера над хоризонта, така както се вижда от FTN, всеки ден в продължение на 21 дни, броено от 27.02.2006 г. На пръв поглед от данните става ясно, че височината на Церера над хоризонта постепенно намалява всеки ден. Кога ще достигне хоризонта?
| Ден | Височина над хоризонта (°) | Ден | Височина над хоризонта (°) |
| 1 | 19 | 12 | 14 |
| 2 | 19 | 13 | 14 |
| 3 | 18 | 14 | 13 |
| 4 | 18 | 15 | 13 |
| 5 | 17 | 16 | 12 |
| 6 | 17 | 17 | 12 |
| 7 | 16 | 18 | 11 |
| 8 | 16 | 19 | 11 |
| 9 | 16 | 20 | 10 |
| 10 | 15 | 21 | 10 |
| 11 | 15 |
а) Начертайте графика с височината на Церера над хоризонта по дни, използвайки данните от таблицата по-горе. Свържете с права начертаните точки.
Решение:
б) Изчислете наклона на правата и пресечната точка с оста y. Ако приемем, че точките могат най-добре да бъдат съединени с права, какво ще е уравнението за тези данни?nbsp;
Решение: Между 1-ия и 21-ия ден (20 дни) разликата във височината е 9 °, т.е. наклонът на правата е 9° / 20 = –0,45°. Пресечната точка с оста y е 19. Линейното уравнение е под формата на y = −0,45x + 19.
в) Определете колко дни Церера ще бъде под хоризонта. (Съвет: Един космически обект залязва, когато височината му над хоризонта е 0°.)
Решение: Церера ще залезе в момента, когато височината и над хоризонта е 0 °, т.е. y = 0. Решаваме уравнението и търсим x, за което y е равно 0. Можем да напишем
0,45x = 19
x = 42
Церера ще залезе след 42 дни.
Задача: Орбитата на планетата-джудже Плутон е различна от орбиталните траектории на планетите – ексцентрицитет 0,25, наклон 17°. Ексцентрицитетът на орбитите на планетите варира от 0,007 (за Венера) до 0,206 (за Меркурий), като повечето планети имат ексцентрицитет по-малък от 0,1. Наклонът на орбитата спрямо еклиптичната равнина варира от 0° (за Земята, по дефиниция на еклиптиката) до 7 ° (за Меркурий). В резултат на това, за определено време Плутон е по-близо до Слънцето (от 07.02.1979 г. до 11.02.1999 г.) отколкото Нептун, имайки предвид проектирането на неговата орбита в равнината на еклиптиката.
а) Да предположим, че Плутон се движи по кръгова орбита. Изчислете с колко процента (каква част) от времето Плутон е по-близо до Слънцето в сравнение с планетата Нептун. Колко дни е това?nbsp;
Решение: Орбиталният период на Плутон е 248 години. Плутон е по-близо между 1979 г. и 1999 г., което е около 20 години. Точността на изчислението е достатъчна за възрастта на учениците, така че 20/248 = 8%. Между 07.02.1979 г. и 11.02.1999 г. ще изминат 7309 дни = 20 години · 365 дни + 5 дни за високосните години (1980, 1984, 1988, 1992 и 1996) + 4 дни (7 дни месечно до 11-ия ден в месеца).
б) На модела на орбитите на Нептун и Плутон се уверете, че Нептун и Плутон не могат да се сблъскат. Направете прост модел на орбитите на Нептун и планетата- джудже Плутон. Начертайте кръг с радиус 7,5 см върху лист хартия А4, за да представите орбитата на Нептун. Изрежете създадения кръг и изрежете процеп в центъра на кръга. На друг лист хартия начертайте орбитата на Плутон, при което ще бъде по-добре, ако нарисувате правоъгълник със страни 19,8 см и 19,2 см - на компютър в някаква програма (например за чертане, рисуване, или в текстов редактор). Начертайте елипса в него така, че тя да докосва всички страни на правоъгълника. Маркирайте с пунктираните линии и двете оси на елипсата. За да получите местоположението на Слънцето, нарисувайте кръг около центъра на дългата страна на правоъгълника с диаметър 19,8 см и намерете пресечната точка с по-дългата ос на елипсата. И накрая, начертайте перпендикуляр към по- дългата ос на елипсата по такъв начин, че да премине през Слънцето. Отпечатайте фигурата в правилния мащаб за формат А4 и изрежете орбитата, включително маркирания перпендикуляр. Пъхнете двата модела на орбитите един в друг така, че да образуват ъгъл от 17°.
Задача: Колко тежите зависи от гравитационната сила на вашето местоположение. Таблицата по-долу показва каква би била гравитационната сила в различни точки на Слънчевата система в сравнение със стойността (1.00) на земната повърхност. Ако някой тежи 100 кг на Земята, на Луната той ще тежи 17 кг. Тази стойност се достига по следния начин: 100 кг („теглото“ на Земята), умножено по 0,17 (гравитационния фактор за Луната) = 17 кг. Трябва да се отбележи, че масата на обектите не се променя на различни места, остава същата. Само тежестта, която зависи от гравитацията, се променя.
Теглото ти на Земята: _ _ _ _ _100 _ _ _ _ _ кг
| Местоположение | Гравитационен фактор на повърхността (на Земята = 1,00) |
Моето „тегло“ на това място |
| Слънце | 28 | 2 800 |
| Меркурий | 0,38 | 38 |
| Венера | 0,9 | 90 |
| Земя | 1,0 | 100 |
| Луна | 0,17 | 17 |
| Марс | 0,38 | 38 |
| Церера |
0,029 | 2,9 |
| Юпитер | 2,53 | 253 |
| Сатурн | 1,1 | 110 |
| Уран | 0,9 | 90 |
| Нептун | 1,14 | 114 |
| Плутон | 0,06 | 6 |
Трябва да се отбележи, че на газовите планети и Слънцето всъщност не може да се стъпи, защото нямат твърда повърхност. Сортирайте местата от списъка с вашето „тегло“ от най-голямото до най-малкото. От кой параметър зависи промяната на Вашето „тегло“?nbsp;
Решение: Слънце, Юпитер, Нептун, Сатурн, Земя, Венера, Уран, Меркурий, Марс, Луна, Плутон, Церера. Промяната зависи от гравитационното ускорение, което се влияе от масата на обекта, неговия размер (гравитационната сила) и времето на въртене около оста, размерите на космическия обект (центробежната сила).
Задача: В тази задача ще разгледаме как теглото на планетата влияе на скока на височина.
Инструкции за работа:
1. Учениците формират групи от по трима.
2. Един ученик от групата държи метъра вертикално на пода, като началото на метъра докосва пода.
3. Вторият ученик в групата наблюдава метъра и записва височината на скока на третия ученик от групата.
4. Третият ученик от групата скача на височина до метъра. Височината на скока се записва и това се повтаря общо три пъти. От трите скока средната височина на скоковете се изчислява и се записва в таблицата, като тя ще се счита за височина на скока на Земята.
5. Учениците си сменят ролите, което означава, че за всеки един скачащ ще бъде записана средната височина на скока му на Земята.
Таблица 1: Изчисляване на средната височина на скока на Земята
| Скок | Опит No 1 | Опит No 2 | Опит No 3 | Среден скок |
| Височина (cm) | 53 | 50 | 47 | 50 |
6. Използвайте Таблица 2 за изчисляване на средната височина на скоковете и на други места в Слънчевата система.
7. Попълнете Таблица 3, като впишете планетите, Слънцето и планетата-джудже Плутон, както и височината на вашите скокове според теглото на космическия обект – от космическия обект с най-малка маса до космическия обект с най- голяма маса.
8. Създайте графика с колонки за височината на скоковете, като редът на космическите обекти се определя от масата на космическите обекти.
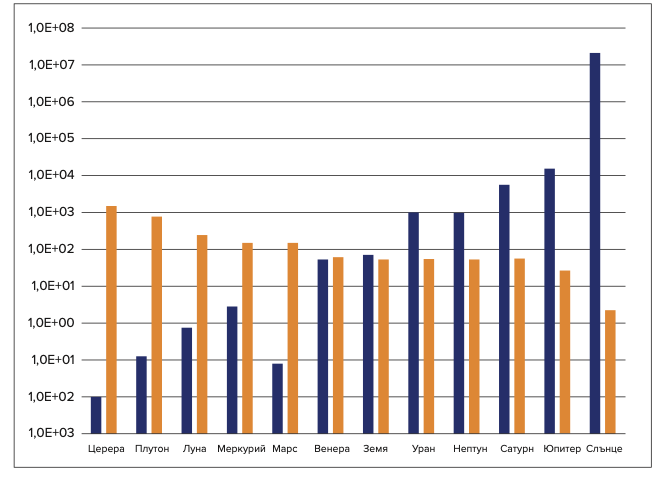
Таблица 2: Как височината на скачане е повлияна от масата на космическия обект от Слънчевата система
| Космически обект |
Тегло на космическия обект от Слънчевата система (× 1023 kg) |
Средна височина на скока на Земята (cm) |
Коефициент на преобразуване за височината на скока |
Височина на скока (cm) |
| Слънце | 19 900 000 | 50 | ×0,036 | 1,8 |
| Меркурий | 3,3 | 50 | ×2,63 | 132 |
| Венера | 48,7 | 50 | ×1,11 | 55,5 |
| Земя | 59,7 | 50 | ×1 | 50 |
| Луна | 0,73 | 50 | ×5,88 | 294 |
| Марс | 6,42 | 50 | ×2,63 | 132 |
| Церера | 0,0094 | 50 | ×34,5 | 1 730 |
| Юпитер |
19 00 | 50 | ×0,40 | 20 |
| Сатурн | 5 680 | 50 | ×0,91 | 46 |
| Уран | 868 | 50 | ×1,11 | 55,5 |
| Нептун | 1 020 | 50 | ×0,88 | 44 |
| Плутон | 0,13 | 50 | ×16,7 | 835 |
Използвайте изброените по-горе маси, за да подредите космическите обекти от Слънчевата система от тези с най-малка маса до тези с най-голяма маса, а след това ги въведете в таблицата по-долу. Въведете височината на скоковете за всеки изброен космически обект от Слънчевата система в таблицата.
Таблица 3: Ред на космическите обекти от Слънчевата система по маса
| Обект на Слънчевата система | Височина на скока върху даден обект |
| Церера |
1 730 |
| Плутон |
835 |
| Луна | 294 |
| Меркурий |
132 |
| Марс |
132 |
| Венера |
55,5 |
| Земя |
50 |
| Уран |
55,5 |
| Нептун |
44 |
| Сатурн |
46 |
| Юпитер |
20 |
| Слънце |
1,8 |
Използвайте данните от таблиците по-горе и създайте диаграма, която сравнява масите на космическите обекти от Слънчевата система и височината на вашите скокове. Подредете космическите обекти от тези с най-малка маса до тези с най- голяма маса по хоризонталната ос.
Решение:
Задача: На кой космически обект от Слънчевата система може да скочите най- високо, къде може да скочите най-малко?
Решение: Най-високо може да скочите на планета-джудже Церера, най-малко на Слънцето, но така или иначе, този космически обект няма твърда повърхност както другите газови планети. Така че за правилен отговор може да се счита Земята.
Задача: Защо е възможно да скочите по-високо на Меркурий, отколкото на Нептун?nbsp;
Решение: На Меркурий върху нас действа по-малката гравитационна сила, така че тук можем да скочим по-високо. Трябва да се отбележи, че Нептун е газообразна планета и няма твърда повърхност.
Задача: Ако искате да подобрите световния рекорд в скока на височина, кой космически обект от Слънчевата система ще си изберете? Защо? На какви космически обекти от Слънчевата система бихте могли да подобрите съществуващия световен рекорд на висок скок?nbsp;
Решение: Бих си избрал(а) планетата-джудже Церера или планетата-джудже Плутон, но поради голямата им отдалеченост от Земята бих предпочел(а) Луната, която е на приблизително 384 хиляди км от Земята. Рекордът може да бъде преодолян на други каменисти планети, т.е. на Меркурий, Венера и Марс.