- Задача 1: Радиани или градуси?
- Задача 2: Марс в опозиция и квадратура
- Задача 3: Измерване на Меркурий и Венера
- Задача 4: „Меркуан“
- Задача 5: Земята от Марс
- Задача 6: Колко голяма е Луната?
- Задача 7: Луната за втори път
- Задача 8: Параметри на орбитите на планетите
- Задача 9: Като от друга планета
- Задача 10: С Краката здраво на земята...
- Задача 11: Гръко, колко голяма е Земята?
- Задача 12: Луната в действие за трети път
Задача 12: Луната в действие за трети път
a) Фигура 26 показва пълно лунно затъмнение. Използвайки Фигура 26 и времената, преценете колко пъти радиусът на сянката на Земята ще е по-голям от радиуса на Луната.
б) Ако ъгловият размер на Слънцето е θ☉ =32‘, радиусът на Земята е R⊕ = 6 378 km а радиусът на кръговата орбита е a2 = 384 400 km, с помощта на горния резултат от точка а), изчислете радиуса на Луната. Фигура 27 може да помогне.
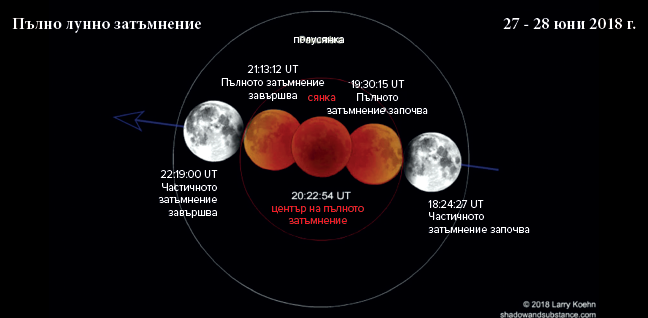
Фиг. 26 Затъмнение на Луната
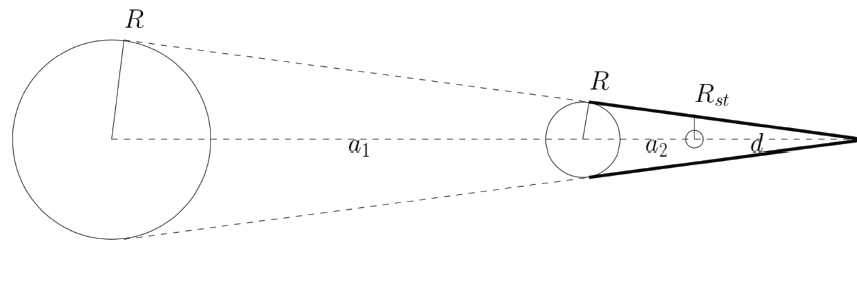
Фиг. 27. Затъмнение на Луната – анализ на ситуацията
Решение
a) От показаните на фигурата времена става ясно, че на Луната ѝ е отнело около 1 час и 6 минути, за да влезе в сянката на Земята. След това остава в тази сянка за около 2 часа и 49 минути. Съотношението на тези времена съответства на съотношението на диаметъра на земната сянка към радиуса на Луната:
Тъй като преминаването на Луната през земната сянка не е точно централно, съотношението всъщност ще бъде малко по-голямо.
б) Скицата предполага следното: . Тъй като лявата страна на първото уравнение може да бъде написана като
, което се равнява на
. От първото уравнение получаваме
. От второто равенство получаваме
. Тогава за радиуса на Луната се получава:
. Истинският радиус на Луната е 1737 км, и следователно полученият резултат е разумен.