ВЪВЕДЕНИЕ
В този текст представяме така наречените „конфигурации“ - отличителните позиции на планетите в Слънчевата система от гледна точка на Земята. Постепенно ще обясним термините: съединение, опозиция, елонгация, квадратура и ще разгледаме как да определяме разстоянието от Земята до планетата, разположена в едно от тези положения.
След това ще обясним как се определя ъгловият размер на тялото и как знанията ни за това, заедно с познаването на разстоянието до тялото, ще ни помогнат да определим истинските размери на тялото. Затова сме принудени да работим с тригонометрични функции. Ще обясним обаче защо в случаите, когато космическите обекти са далеч от наблюдателя, можем да игнорираме тригонометричните функции и да опростим изчисленията. За тази цел естествено въвеждаме много полезни ъглови единици, наречени радиани.
Разстояния и величини
Типични разстояния в Слънчевата система
Средното разстояние Земя – Слънце е 1 au ≐ 1,496 ∙ 108 km, радиусът на Земята е km. Таблица 1 показва средните разстояния на планетите от Слънцето и техните радиуси в кратни радиуси на Земята. Радиусът на Слънцето също е даден за сравнение. Размерите на Слънцето изглеждат огромни в сравнение с другите планети, но е интересно да се изчисли радиусът на Слънцето в астрономически единици:
. Това показва, че планетите и Слънцето не заемат голяма част от пространството в Слънчевата система.
Таблица 1: Средните разстояния на планетите в Слънчевата система и радиусите на планетите и Слънцето
| Тяло |
Разстояние от Слънцето [au] |
R/R⊕ |
| Слънце |
0 | 109 |
| Меркурий |
0,39 | 0,38 |
| Венера |
0,72 | 0,95 |
Земя |
1,00 | 1,00 |
| Марс |
1,52 | 0,53 |
| Юпитер | 5,20 | 11,2 |
| Сатурн |
9,54 | 9,45 |
| Уран |
19,2 | 4,01 |
| Нептун | 30,07 | 3,88 |
Конфигурации на планетите
От гледна точка на Земята могат да се разграничат няколко значими позиции на планетата, наречени конфигурации, които са схематично представени на Фиг.19 и тяхното описание е дадено по-долу.
1. Съединение
При вътрешните планети (Меркурий, Венера) разпознаваме горно и долно съединение. Горното съединение е моментът, когато планетата се намира в противоположната страна на Слънцето (Слънцето е между Земята и вътрешната планета). Долното съединение възниква, когато планетата е между Земята и Слънцето. Външните планети (Марс, Юпитер, Сатурн, Уран, Нептун) могат да бъдат само в горно съединение.
Ако планетата е в съединение, тя изгрява и залязва заедно със Слънцето, намира се на дневното небе и не е наблюдаема за нас.
2. Опозиция
Моментът, в който външната планета е най-близо до Земята, съответно Земята е между планетата и Слънцето, се нарича опозиция. По време на опозицията са най- добрите условия за наблюдение на планетата, защото планетата изгрява при залез и залязва при изгрев Слънце (планетата е наблюдаема през цялата нощ). Тогава, гледана през телескоп, планетата изглежда и най-голяма (има най-голям ъглов размер).
3. Елонгация
Елонгацията е ъгловото разстояние между вътрешната планета и Слънцето. При западна елонгация на планетата тя изгрява и залязва преди Слънцето. При източна елонгация на планетата тя изгрява и залязва след Слънцето. Най-голямото ъглово разстояние на планетата от Слънцето се нарича максимална елонгация. Максималната елонгация на Меркурий е 23°, на Венера е 47°
4. Квадратура
Квадратура е моментът, когато ъгълът Слънце – Земя – външна планета е прав. В квадратура могат да се намират само външните планети.
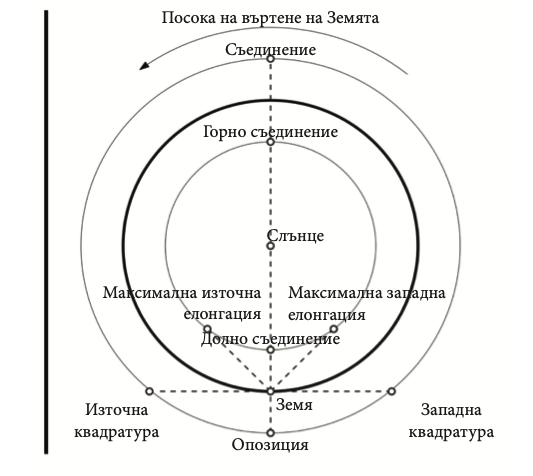
Фигура 19: Диаграма на възможните конфигурации на планетите
Ъглови размери на космическите обекти
Естествено е, че ако космическите обекти са по-далеч от нас, те изглеждат по-малки, отколкото ако бяха в наша непосредствена близост. Въпреки това физическите им измерения не се променят. За да можем да опишем този факт по-качествено, въвеждаме величината „ъглов размер“, чието значение е показано на Фиг. 20. Показаното на фигурата ни дава ясна представа как да изчисляваме ъгловия размер:
След това ъгълът се получава като: . Тогава, за Слънцето с радиус
, получаваме ъглов размер, θ☉ ≐ 32'. Едва ли е изненадващо, че след това ъгловите размери на планетите в Слънчевата система се получават в единици от десетки ъглови секунди.
След това ще покажем как да опростим отношението за изчисляване на ъгловия размер, ако ъгловият размер е много малък. Това ще изисква въвеждането на „нови“ равнинни ъглови единици, така наречените „радиани“.
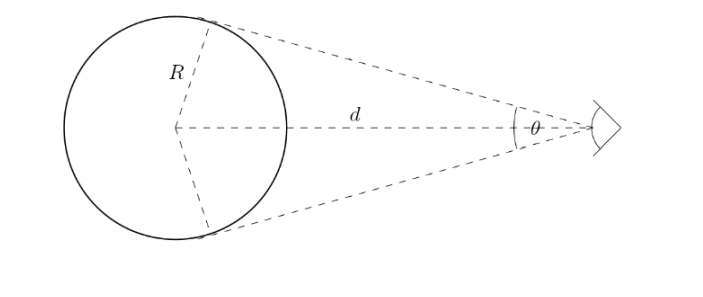
Фигура 20: Дефиниция на ъгловия размер
Радиани
Радианите са най-естествено дефинираните единици за равнинния ъгъл. Нека си представим окръжности, както на фигура 3. Ъгълът се определя като съотношението на дължината, отговарящо на съответната дъга и радиуса на окръжността. От фигура 3 се вижда, че ъгълът не зависи от определена дължина или от радиуса:
, тя се определя като съотношението на дължината на съответната дъга към радиуса на окръжността. От Фиг. 21 се вижда, че ъгълът не зависи от определена дължина или радиуса, a само от тяхното съотношение, което е естествено и правилно. Вече знаем как да определим ъгъл, но все още не знаем какво е „радиан“.
От определението за ъгъла (дължина на дъгата, разделена на радиуса), изглежда, че ъгълът не е оразмерен или, че единицата на ъгъла е „единица“. Точно това се нарича „радиан“! Бихме могли да напишем също:. Има много безразмерни числа. Пишейки „rad“ към числата, ние всъщност посочваме, че числото съответства на размера на ъгъла.
Тъй като обиколката (дължината) на окръжността е , тя е пълен ъгъл
. Разбира се,
. Предпоследното равенство ни дава връзката за преобразуване между радиани и градуси:
.
Освен това, ние трябва да отбележим, че колкото по-малък е ъгълът, толкова по- малка е дъгата. Ще използваме това в следващия параграф.
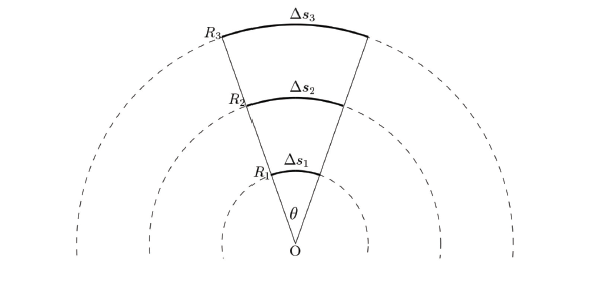
Фигура 21: Въвеждане на радианите
Ъглов размер за втори път
Сега си представете, че размерът на сферичен космически обект е значително по-малък от разстоянието му от нас. Както е посочено по-горе, поради големите разстояния (достатъчно малка) дъга може да бъде заместена от отсечка и обратно. В този случай е възможно за ъгловия размер на космическия обект (в радиани) да напишем
Разбира се, за малките ъглови размери отношението трябва да даде същите резултати както преди това , (калкулаторът може да изчисли тангенса в градуси и в радиани).
Източници и препоръчана литература
[1] Mikulčák J., Macháček M., Zemánek F.: Matematické, fyzikální a chemické tabulky
a vzorce pro SŠ, Prometheus, Praha, 2003
[2] Široký J., Široká M.: Základy astronomie v příkladech, SPN, Praha, 1966, online odkaz:
http://physics.ujep.cz/~zmoravec/astronomie/siroky/siroky.html, cit. 8.7.2018