- Задача 1: Радиани или градуси?
- Задача 2: Марс в опозиция и квадратура
- Задача 3: Измерване на Меркурий и Венера
- Задача 4: „Меркуан“
- Задача 5: Земята от Марс
- Задача 6: Колко голяма е Луната?
- Задача 7: Луната за втори път
- Задача 8: Параметри на орбитите на планетите
- Задача 9: Като от друга планета
- Задача 10: С Краката здраво на земята...
- Задача 11: Гръко, колко голяма е Земята?
- Задача 12: Луната в действие за трети път
Задача 6: Колко голяма е Луната?
a) Средното разстояние между Земята и Слънцето е d = 1 au = 1,496 ⋅ 108 km, радиусът на Слънцето е R☉ = 6,955 ⋅ 105 km. Определете ъгловия размер на Слънцето за един наблюдател на Земята.
б) Като знаем масата на Земята M⊕ = 5,97 ⋅ 1024 kg и орбиталния период на Луната около Земята T = 27,3 дни и използвайки третия закон на Кеплер, изчислете разстоянието на Луната от Земята. Пренебрегнете масата на Луната за определяне на разстоянието.
в) Тъй като знаете, че има както частични, така и пълни слънчеви затъмнения, определете истинските размери на Луната. Илюстрация на явлението е показана на Фиг. 23.

Фигура 23 (Източник: https://apod.nasa.gov/apod/ap160831.html, cit. 5.8.2018)

Фиг. 24 (Източник: https://www.nasa.gov/multimedia/ imagegallery/image_feature_1249.html,cit. 5.8.2018)
г) Какъв би бил ъгловият размер на Земята за астронавт на Луната, ако Луната се движеше по точно кръгова орбита? Каква част от земната повърхност вижда астронавтът (Фиг. 24 и 25)? Изразете резултата като процент. Радиусът на Земята е R⊕ = 6 378 km.
Съвет: Частта от земната повърхност, която наблюдателят вижда, съответства на повърхността на сферичния ъгъл. Площта на сферичния ъгъл (без основата) е , където R е радиусът на сферата, a v е височината на сферичния сегмент, вж. Фигура 4.
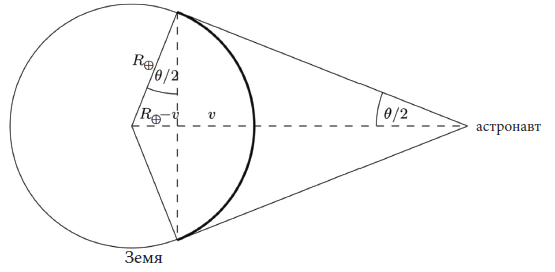
Фиг. 25. Илюстрация на гледката на астронавта към Земята
Решение
a) Изхождаме от приблизителното отношение за ъглов размер:.
Можем да изходим и от точната връзка
респективно.
.
Резултатите, разбира се, са същите, вж. Задача 1.
б) Започваме от Третия закон на Кеплер: .
в) Тъй като има частични и пълни слънчеви затъмнения, ъгловият размер на Луната е сравнима с ъгловия размер на Слънцето, т.е. . Определяме радиуса на Луната от съотношението:
.
Истинският радиус на Луната е 1,737 км, така че резултатът ни съответства на реалността.
г) Изхождаме от приблизителното отношение за ъглов размер: .
От Фигура 20 става ясно, че:
. Можем да изчислим големината на сферичния ъгъл или директно от определени стойности, или от изчислената стойност на ъгловия размер на Земята. Заменяме в спомагателната формула за областта на сферичния ъгъл
. Формула за площта на сферата е
, затова за съотношението на площта на сферичния ъгъл към цялата сфера важи:
. Астронавтът вижда почти една цяла страна на Земята.
От последното уравнение става ясно, че колкото по-далеч астронавтът е от Земята (разстоянието е дадено от голямата полуос, тъй като съответства на радиуса на кръговата орбита), то тогава членът ще бъде по-близко до нулата и астронавтът ще види по-голяма част от Земята, но максимално 50 %. Ако, напротив, астронавтът е точно над земната повърхност, то членът ще бъде
бъде близо до 1 и съотношението ще бъде
нула.